题目内容
(本小题满分12分) 已知数列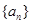 是公差不为
是公差不为 的等差数列,其前
的等差数列,其前 项和为
项和为 ,且
,且 成等比数列.
成等比数列.
(Ⅰ)求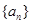 的通项公式;
的通项公式;
(Ⅱ)是否存在正整数 ,使
,使 仍为数列
仍为数列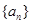 中的一项?若存在,求出满足要求的所有正整数
中的一项?若存在,求出满足要求的所有正整数 ;若不存在,说明理由.
;若不存在,说明理由.
【答案】
解:(Ⅰ)设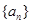 的公差为
的公差为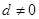 ,则
,则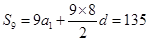 ,
,
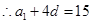 ………………①
………………①
又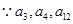 成等比数列,
成等比数列,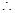
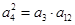 ,即
,即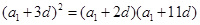 ,
,
化简,得 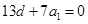 ………………②
………………②
由①②,得: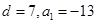 ,
, 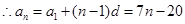 . ………………………6分
. ………………………6分
(Ⅱ)由于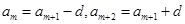 ,
,
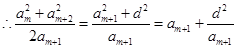 ,
,
设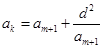 , 则
, 则 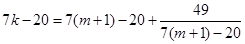 ,
,
即 ,由于
,由于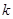 、
、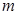 为正整数,所以
为正整数,所以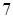 必须能被
必须能被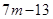 整除,
整除,
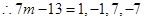 ,
,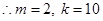 ,
,
故存在唯一的正整数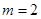 ,使
,使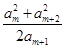 仍为
仍为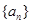 中的一项.………………12分
中的一项.………………12分
【解析】略

练习册系列答案
相关题目