摘要:21.(本题满分16分.其中第小题8分) 已知存在实数(其中)使得函数是奇函数.且在上是增函数. (1)试用观察法猜出两组与的值.并验证其符合题意, (2)求出所有符合题意的与的值.
网址:http://m.1010jiajiao.com/timu3_id_502485[举报]
(本题满分16分,其中第(1)小题4分,第(2)小题8分,第(3)小题4分)
设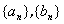 是两个数列,
是两个数列, 为直角坐标平面上的点.对
为直角坐标平面上的点.对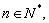 若三点
若三点 共线,
共线,
(1)求数列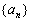 的通项公式;
的通项公式;
(2)若数列{ }满足:
}满足: ,其中
,其中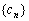 是第三项为8,公比为4的等比数列.求证:点列
是第三项为8,公比为4的等比数列.求证:点列 (1,
(1,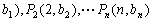 在同一条直线上;
在同一条直线上;
(3)记数列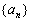 、{
、{ }的前
}的前 项和分别为
项和分别为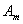 和
和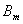 ,对任意自然数
,对任意自然数 ,是否总存在与
,是否总存在与 相关的自然数
相关的自然数 ,使得
,使得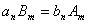 ?若存在,求出
?若存在,求出 与
与 的关系,若不存在,请说明理由.
的关系,若不存在,请说明理由.
查看习题详情和答案>>
(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.已知函数![]() (其中
(其中![]() 且
且![]() ,
,![]() 为实数常数).
为实数常数).
(1)若![]() ,求
,求![]() 的值(用
的值(用![]() 表示);
表示);
(2)若![]() 且
且![]() 对于
对于![]() 恒成立,求实数m的取值范围(用
恒成立,求实数m的取值范围(用![]() 表示).
表示).
 (其中
(其中 且
且 ,
, 为实数常数).
为实数常数). ,求
,求 的值(用
的值(用 且
且 对于
对于 恒成立,求实数m的取值范围(用
恒成立,求实数m的取值范围(用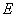 的方程为
的方程为 ,长轴是短轴的2倍,且椭圆
,长轴是短轴的2倍,且椭圆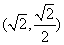 ;斜率为
;斜率为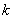 的直线
的直线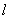 过点
过点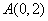 ,
,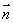 为直线
为直线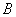 满足条件
满足条件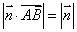 .
.