摘要:(1)常数T满足 和,则T的一个值是( ). (A) (B) (C) (D) 2)在等差数列 中. ,则 的值为( ). 20 (D) (3)设点P对应复数是,以原点为极点.实轴的正半轴为极轴.建立极坐 标系.则点P的极坐标为( ). (A) (B) (C) (D) (4)设A.B是两个非空集合.若规定:,则等于( ) (A) (B) (C) (D) (5)函数的图象与直线的交点个数为( ). 0或1 (6)设函数(其中),则是为 奇函数的( ). 必要不充分条件 既不充分也不必要条件 (7)如图.在斜三棱柱中.∠BAC=90°..过作 底面ABC.垂足为.则( ). (A)在直线AC上 (B)在直线AB上 (C)在直线BC上 (D)在△ABC内 (8)电讯资费调整后.市话费标准为:通话时间不超过3分钟收费0.2元,超 过3分钟.以后每增加1分钟收费0.1元.不足1分钟以1分钟收费.则通话收S(元)与通话时间t的函数图象可表示为( ). (9)以椭圆的右焦点为圆心.且与双曲线的渐近线相 切的圆的方程为( ). (A) (B) (C) (D) (10)已知的展开式中所有项系数之和为729.则这个展开式中含项 的系数是( ). 160 (D)180 (11)AB是过圆锥曲线焦点F的弦.l是与点F对应的准线.则以弦AB为直 径的圆与直线l的位置关系( ). 相离 (D)由离心率e决定 (12)定义在R上的函数的反函数为.则是( ). 偶函数 ( C)非奇非偶函数 (D)满足题设的函数不存在
网址:http://m.1010jiajiao.com/timu3_id_502402[举报]
设有两组数据x1,x2,…,xn与y1,y2, …,yn,它们的平均数分别是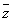 和
和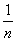 ,则新的一组数据2x1-3y1+1,2x2-3y2+1,…,2xn-3yn+1的平均数是( )
,则新的一组数据2x1-3y1+1,2x2-3y2+1,…,2xn-3yn+1的平均数是( )
A.2![]() -3
-3![]() B.2
B.2![]() -3
-3![]() +1 C.4
+1 C.4![]() -9
-9![]() D.4
D.4![]() -9
-9![]() +1
+1
(本小题满分12分)
已知定理:若“![]() 为常数,
为常数,![]() 满足
满足![]() ,则函数
,则函数![]() 的图象关于点
的图象关于点![]() 中心对称。”设函数
中心对称。”设函数![]() ,定义域为A。
,定义域为A。
(1)证明:函数![]() 的图象关于点
的图象关于点![]() 中心对称;
中心对称;
(2)当![]() 时,求函数值
时,求函数值![]() 的取值范围;
的取值范围;
(3)对于给定的![]() ,设计构造过程:
,设计构造过程:![]() ,若
,若![]() ,构造过程将继续下去;若
,构造过程将继续下去;若![]() ,构造过程都可以无限进行下去,求
,构造过程都可以无限进行下去,求![]() 的值。
的值。
以下有四种说法:
①若p或q为真,p且q为假,则p与q必为一真一假;
②若数列![]() 的前n项和为Sn=n2+n+l,n∈N*,则
的前n项和为Sn=n2+n+l,n∈N*,则![]() ∈N*
∈N*
③若实数t满足![]() ,则称t是函数f(x)的一个次不动点.设函数f(x)=Inx与函数g(x)=ex(其中e为自然对数的底数)的所有次不动点之和为m,则m=0
,则称t是函数f(x)的一个次不动点.设函数f(x)=Inx与函数g(x)=ex(其中e为自然对数的底数)的所有次不动点之和为m,则m=0
④若定义在R上的函数f(x)满足![]() ,则6为函数f(x)的周期
,则6为函数f(x)的周期
以上四种说法,其中说法正确的是
A.①③ B.③④ C.①②③ D.①③④
查看习题详情和答案>>已知函数y=2sin2(x+
)-cos2x,则它的周期T和图象的一条对称轴方程是( )
| π |
| 4 |
A、T=2π,x=
| ||
B、T=2π,x=
| ||
C、T=π,x=
| ||
D、T=π,x=
|