摘要：证(Ⅰ)∵PA^底面ABCD AD是PD在平面ABCD内的射影. ∵CDÌ平面ABCD.且CD^AD. 故CD^PD ．------...-4分 (Ⅱ)取CD中点G.连结EG.FG ∵E.F分别是AB.PC的中点.\EG//AD.FG//PD. \平面EFG//平面PAD.\EF//平面PAD． -----..--8分 (Ⅲ)当平面PCD与平面ABCD成45°角时.直线EF^平面PCD. 证明:G为CD中点.则EG^CD.由(1)知FG^CD. 故ÐEGF为平面PCD 与平面ABCD所成二面角的平面角.即ÐEGF=45°. 从而得ÐADP=45°. AD=AP. 由RtDPAE@RtDCBE.得PE=CE. 又F是PC的中点.\EF^PC. 由CD^EG.CD^FG.得CD^平面EFG.CD^EF.即EF^CD. 故EF^平面PCD． ----..------.----.12分
网址：http://m.1010jiajiao.com/timu3_id_502105[举报]
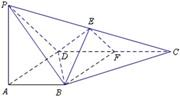如图，在四棱锥P-ABCD中，PA⊥底面ABCD，∠DAB为直角，AB∥CD，AD=CD=2AB，E、F分别为PC、CD的中点．（Ⅰ）试证：AB⊥平面BEF；
（Ⅱ）设PA=k•AB，且二面角E-BD-C的平面角大于45°，求k的取值范围． 查看习题详情和答案>>
底面ABCD为矩形的四棱锥P-ABCD中，AB=| 3 |
（Ⅰ）求直线AC与PB所成角的余弦值；
（Ⅱ）在侧面PAB内找一点N，使NE⊥面PAC，并求出点N到AB和AP的距离．
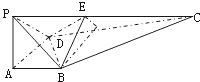如图，在四棱锥P-ABCD中，PA⊥底面ABCD，∠DAB为直角，AB∥CD，AD=CD=2AB，E、F分别为PC、CD中点．（Ⅰ）试证：CD⊥平面BEF；
（Ⅱ）高PA=k•AB，且二面角E-BD-C的平面角大于30°，求k的取值范围． 查看习题详情和答案>>
底面ABCD,
DAB为直角，AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.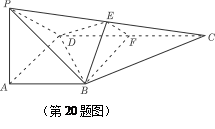
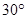,求k的取值范围.
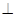底面ABCD,
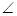DAB为直角，AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.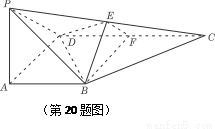
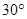,求k的取值范围.