摘要: 解:上的单调 递增区间为 10.解析:(1)设----1分 ----4分 ∴ ∴ ----6分 (2) 对任意的 ----8分 ∵, 当x=1时或3时., 当 ∴上的最大值为的取值范围是.-12分
网址:http://m.1010jiajiao.com/timu3_id_501989[举报]
已知函数f(x)=
asinωx•cosωx-cos2ωx+
(ω∈R+,a∈R)的最小正周期为π,其图象关于直线x=
对称.
(1)求函数f(x)在[0,
]上的单调递增区间;
(2)若关于x的方程1-f(x)=m在[0,
]上只有一个实数解,求实数m的取值范围.
查看习题详情和答案>>
| 3 |
| 3 |
| 2 |
| π |
| 6 |
(1)求函数f(x)在[0,
| π |
| 2 |
(2)若关于x的方程1-f(x)=m在[0,
| π |
| 2 |
给出下列四个命题,其中错误的命题有( )个.
(1)将函数y=sin(2x+
)的图象向右平移
个单位,得到函数y=sin2x的图象;
(2)函数y=sin2x+cos2x在x∈[0,
]上的单调递增区间是[0,
];
(3)设A、B、C∈(0,
)且sinA-sinC=sinB,cosA+cosC=cosB,则B-A等于-
;
(4)方程sin2x+2sinx+a=0有解,则a的取值范围是[-3,1].
(5)在同一坐标系中,函数y=sinx与函数y=
的图象有三个交点.
(1)将函数y=sin(2x+
| π |
| 3 |
| π |
| 3 |
(2)函数y=sin2x+cos2x在x∈[0,
| π |
| 2 |
| π |
| 8 |
(3)设A、B、C∈(0,
| π |
| 2 |
| π |
| 3 |
(4)方程sin2x+2sinx+a=0有解,则a的取值范围是[-3,1].
(5)在同一坐标系中,函数y=sinx与函数y=
| x |
| 2 |
查看习题详情和答案>>
 的最小正周期为π,其图象关于直线
的最小正周期为π,其图象关于直线 对称.
对称. 上的单调递增区间;
上的单调递增区间; 上只有一个实数解,求实数m的取值范围.
上只有一个实数解,求实数m的取值范围.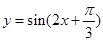 的图象向右平移
的图象向右平移 个单位,得到函数
个单位,得到函数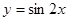 的图象;
的图象;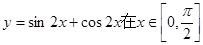 上的单调递增区间是
上的单调递增区间是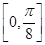 ;
;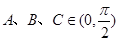 且
且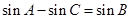 ,
,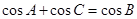 ,则
,则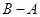 等于
等于 ;
; 有解,则
有解,则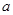 的取值范围是
的取值范围是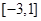 .
.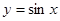 与函数
与函数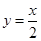 的图象有三个交点;
的图象有三个交点;