摘要:解:(1)设动点N(x, y).则M(-x, 0),P(0, ) (x>0). ∵PM⊥PF.∴kPM·kPF=-1.即 ∴y2=4x(x>0)即为所求. (2)设直线l方程为y=kx+b , 点A(x1, y1) B(x2, y2), 则由=-4.得x1x2+y1y2=-4,即+y1y2=-4 ∴y1y2=-8 由 当△=16-16kb=16(1+2k2)>0时. ∴≤k≤1.或-1≤k≤-, 即所求k的取值范围是.
网址:http://m.1010jiajiao.com/timu3_id_501941[举报]
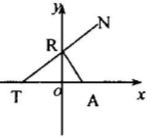 如图所示,点A(1,0).点R在y轴上运动,T在x轴上,N为动点,且
如图所示,点A(1,0).点R在y轴上运动,T在x轴上,N为动点,且| RT |
| RA |
| RN |
| RT |
(1)设动点N的轨迹为曲线C,求曲线C的方程;
(2)过点B(-2,0)的直线l与曲线C交于点P、Q,若在曲线C上存在点M,使得△MPQ为以PQ为斜边的直角三角形,求直线l的斜率k的取值范围. 查看习题详情和答案>>
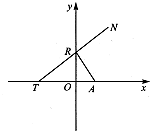 如图所示,点A(p,o)(p>0),点R在y轴上运动,点T在x轴上,N为动点,且
如图所示,点A(p,o)(p>0),点R在y轴上运动,点T在x轴上,N为动点,且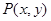 满足
满足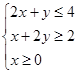 ,则
,则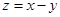 的最小值是( )
的最小值是( )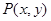 满足
满足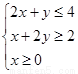 ,则
,则 的最小值是( )
的最小值是( )