题目内容
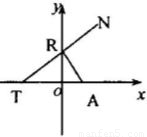
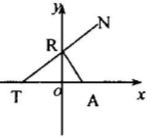 如图所示,点A(1,0).点R在y轴上运动,T在x轴上,N为动点,且
如图所示,点A(1,0).点R在y轴上运动,T在x轴上,N为动点,且| RT |
| RA |
| RN |
| RT |
(1)设动点N的轨迹为曲线C,求曲线C的方程;
(2)过点B(-2,0)的直线l与曲线C交于点P、Q,若在曲线C上存在点M,使得△MPQ为以PQ为斜边的直角三角形,求直线l的斜率k的取值范围.
分析:(1)设N(x,y),由题得R是TN的中点所以T(-x,0),R(0,
),代入
•
=0?(-X,-
)•(1,-
)=0得点N的轨迹曲线C的方程y2=4x
(2)直线l与曲线C交于点P、Q所以直线l的斜率不等于0,设其为x=my-2,代入曲线C的方程y2=4x,△=16m2-32>0,即m2>2,因为△MOQ是以PQ为斜边的直角三角形,所以MP⊥MQ∴
•
=0,即(x1-
)(x2-
)+(y1-t)(y2-t)=0,化简可得8+4mt+t2+16=0关于t的方程t2+4mt+24=0有实根,∴△=16m2-96≥0,又k=
所以-
≤k<0或0<k≤
.
| y |
| 2 |
| RT |
| RA |
| y |
| 2 |
| y |
| 2 |
(2)直线l与曲线C交于点P、Q所以直线l的斜率不等于0,设其为x=my-2,代入曲线C的方程y2=4x,△=16m2-32>0,即m2>2,因为△MOQ是以PQ为斜边的直角三角形,所以MP⊥MQ∴
| MP |
| MQ |
| t2 |
| 4 |
| t2 |
| 4 |
| 1 |
| m |
| ||
| 6 |
| ||
| 6 |
解答: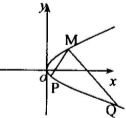 解:(1)设N(x,y),由
解:(1)设N(x,y),由
+
=0知:R是TN的中点,
则T(-x,0),R(0,
),
•
=0?(-X,-
)•(1,-
)=0
则y2=4x就是点N的轨迹曲线C的方程:
(2)设直线l的方程为x=my-2,代入曲线C的方程y2=4x,
得y2-4my+8=0,此方程有两个不等实根,△=16m2-32>0,即m2>2
M在曲线C上,P、Q是直线l与曲线C的交点,设M(
,t),P(x1,y1),Q(x2,y2),
则y1+y2=4m,y1y=8,∵△MOQ是以PQ为斜边的直角三角形,
∴MP⊥MQ∴
•
=0,即(x1-
)(x2-
)+(y1-t)(y2-t)=0
且x1=
,x2=
,
∴
(y12-t2)(y22-t2)+(y1-t)=0,
显然y1-t≠0,y2-t≠0,
∴(y1+t)(y2+t)+16=0,y1•y2+(y1+y2)t+t2+16=0,∴8+4mt+t2+16=0t为点M的坐标,
∴关于t的方程t2+4mt+24=0有实根,∴△=16m2-96≥0.
∴m2≥6,直线l的斜率k=
,∴k≠0且k2≤
,∴-
≤k<0或0<k≤
 解:(1)设N(x,y),由
解:(1)设N(x,y),由| RN |
| RT |
则T(-x,0),R(0,
| y |
| 2 |
| RT |
| RA |
| y |
| 2 |
| y |
| 2 |
则y2=4x就是点N的轨迹曲线C的方程:
(2)设直线l的方程为x=my-2,代入曲线C的方程y2=4x,
得y2-4my+8=0,此方程有两个不等实根,△=16m2-32>0,即m2>2
M在曲线C上,P、Q是直线l与曲线C的交点,设M(
| t2 |
| 4 |
则y1+y2=4m,y1y=8,∵△MOQ是以PQ为斜边的直角三角形,
∴MP⊥MQ∴
| MP |
| MQ |
| t2 |
| 4 |
| t2 |
| 4 |
且x1=
| y12 |
| 4 |
| y22 |
| 4 |
∴
| 1 |
| 16 |
显然y1-t≠0,y2-t≠0,
∴(y1+t)(y2+t)+16=0,y1•y2+(y1+y2)t+t2+16=0,∴8+4mt+t2+16=0t为点M的坐标,
∴关于t的方程t2+4mt+24=0有实根,∴△=16m2-96≥0.
∴m2≥6,直线l的斜率k=
| 1 |
| m |
| 1 |
| 6 |
| ||
| 6 |
| ||
| 6 |
点评:本题考查了利用相关点代入法求曲线的方程重点考查三角形的形状的构成问题.解决此类问题的关键是结合曲线的形状和性质灵活表达垂直关系.

练习册系列答案
相关题目
 (2010•永州一模)如图所示,点A(1,0),B是曲线y=3x2+1上一点,向矩形OABC内随机投一点(该点落在矩形中任一点是等可能的),则所投点落在图中阴影内的概率为( )
(2010•永州一模)如图所示,点A(1,0),B是曲线y=3x2+1上一点,向矩形OABC内随机投一点(该点落在矩形中任一点是等可能的),则所投点落在图中阴影内的概率为( )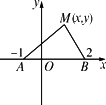
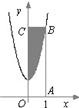 如图所示,点A(1,0),B是曲线y=3x2+1上一点,向矩形OABC内随机投一点(该点落在矩形中任一点是等可能的),则所投点落在图中阴影内的概率为
如图所示,点A(1,0),B是曲线y=3x2+1上一点,向矩形OABC内随机投一点(该点落在矩形中任一点是等可能的),则所投点落在图中阴影内的概率为



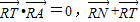 =0,
=0,