题目内容
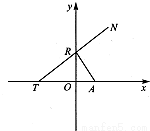
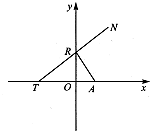 如图所示,点A(p,o)(p>0),点R在y轴上运动,点T在x轴上,N为动点,且
如图所示,点A(p,o)(p>0),点R在y轴上运动,点T在x轴上,N为动点,且| RT |
| RA |
| RN |
| RT |
(I)设动点N的轨迹为曲线C,求曲线C的方程;
(II)设P,Q是曲线C上的两个动点,M(x0,y0)是曲线C上一定点,若
| PM |
| QM |
分析:(I)设N(x,y),由
+
=0知R是TN的中点,则T(-x,0),R(0,
),由
•
=0,知(-x,-
)•(p,
)=0,由此能求出点N的轨迹曲线C的方程.
(II)设P(
,y1),Q(
,y2),则kPQ=
=
,kMP=
.由
•
=0,得PM⊥QM,kMP•kMQ=-1,
•
=-1,由此能推导出直线PQ经过定点(x0+4p,-y0).
| RN |
| RT |
| y |
| 2 |
| RT |
| RA |
| y |
| 2 |
| y |
| 2 |
(II)设P(
| y12 |
| 4p |
| y22 |
| 4p |
| y1- y2 | ||||
|
| 4p |
| y1+ y2 |
| 4p |
| y0+ y2 |
| PM |
| QM |
| 4p |
| y0+y1 |
| 4p |
| y0+y2 |
解答:解:(I)设N(x,y),由
+
=0知R是TN的中点,
则T(-x,0),R(0,
),
∵
•
=0,
∴(-x,-
)•(p,
)=0,
整理,得y2=4px(p>0).
故点N的轨迹曲线C的方程是y2=4px(p>0).
(II)设P(
,y1),Q(
,y2),
则kPQ=
=
,
kMP=
.
由
•
=0,得PM⊥QM,
∴kMP•kMQ=-1,
∴
•
=-1,
从而(-1)(y0+y1)(y0+y2)=16p2.
∴(y1+y2)y0+y1y2+y02+16p2=0.①
直线PQ的方程为y-y1=
(x-
),
即(y1+y2)y-y1y2-4px=0.
①可变为(y1+y2)(-y0)-y1y2-4p(x0+4p)=0,
∴直线PQ经过定点(x0+4p,-y0).
| RN |
| RT |
则T(-x,0),R(0,
| y |
| 2 |
∵
| RT |
| RA |
∴(-x,-
| y |
| 2 |
| y |
| 2 |
整理,得y2=4px(p>0).
故点N的轨迹曲线C的方程是y2=4px(p>0).
(II)设P(
| y12 |
| 4p |
| y22 |
| 4p |
则kPQ=
| y1- y2 | ||||
|
| 4p |
| y1+ y2 |
kMP=
| 4p |
| y0+ y2 |
由
| PM |
| QM |
∴kMP•kMQ=-1,
∴
| 4p |
| y0+y1 |
| 4p |
| y0+y2 |
从而(-1)(y0+y1)(y0+y2)=16p2.
∴(y1+y2)y0+y1y2+y02+16p2=0.①
直线PQ的方程为y-y1=
| 4p |
| y1 +y2 |
| y12 |
| 4p |
即(y1+y2)y-y1y2-4px=0.
①可变为(y1+y2)(-y0)-y1y2-4p(x0+4p)=0,
∴直线PQ经过定点(x0+4p,-y0).
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与抛物线的相关知识,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
相关题目
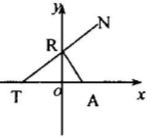 如图所示,点A(1,0).点R在y轴上运动,T在x轴上,N为动点,且
如图所示,点A(1,0).点R在y轴上运动,T在x轴上,N为动点,且
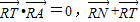 =0,
=0,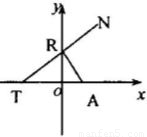
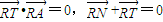 .
.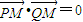 ,试证明直线PQ经过定点,并求出该定点的坐标.
,试证明直线PQ经过定点,并求出该定点的坐标.