题目内容
(08年福建卷理)(本小题满分12分)
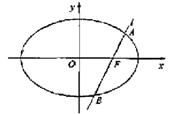
如图,椭圆![]() 的一个焦点是
的一个焦点是![]() ,O为坐标原点.
,O为坐标原点.
(Ⅰ)已知椭圆短轴的两个三等分点与一个焦点构成正三角
形,求椭圆的方程;
(Ⅱ)设过点F的直线l交椭圆于A、B两点.若直线l绕点F
任意转动,恒有![]() ,求a的取值范围.
,求a的取值范围.

解析:本小题主要考查直线与椭圆的位置关系、不等式的解法等基本
知识,考查分类与整合思想,考查运算能力和综合解题能力。满分12分。
解法一:(Ⅰ)设M,N为短轴的两个三等分点,
因为△![]() 为正三角形,
为正三角形,
所以![]() ,
,
即![]()
![]() 因此,椭圆方程为
因此,椭圆方程为![]()
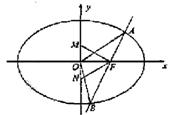
(Ⅱ) 设![]()
() 当直线 ![]() 与
与![]() 轴重合时,
轴重合时,
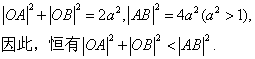
() 当直线![]() 不与
不与![]() 轴重合时,
轴重合时,
设直线![]() 的方程为:
的方程为:![]()
整理得![]()
所以![]()
因为恒有![]() ,所以
,所以![]() 恒为钝角.
恒为钝角.
即![]() 恒成立.
恒成立.
![]()

又![]() ,所以
,所以![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,
恒成立,
当![]() 时,
时,![]() 最小值为0,
最小值为0,
所以![]() ,
, ![]() ,
,![]()
因为![]() 所以
所以![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍去),即
(舍去),即![]() .
.
综合(i)(ii),a的取值范围为![]() .
.
解法二:
(Ⅰ)同解法一.
(Ⅱ) 解:()当直线![]() 垂直于
垂直于![]() 轴时,
轴时,
![]() 代人
代人![]() ,
,![]() .
.
因为恒有![]() ,
,![]() ,即
,即![]() ,
,
解得![]() 或
或![]() (舍去),即
(舍去),即![]() .
.
() 当直线![]() 与不垂直于
与不垂直于![]() 轴时,
轴时,
设直线![]() 的方程为
的方程为![]() 代入
代入![]() .
.
得![]() ,
,
故![]()
因为恒有![]() ,
,
所以![]() ,
,
得![]() 恒成立。
恒成立。
![]()
![]()
由题意得![]() 对
对![]() 恒成立。
恒成立。
① 当![]() 时,不合题意;
时,不合题意;
② 当![]() 时,
时,![]() ;
;
③ 当![]() 时,
时,![]() ,
,
解得![]() 或
或![]() (舍去),即
(舍去),即![]() ,因此
,因此![]() .
.
综合(i)(ii),a的取值范围为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案