摘要：22． (理)对于在区间[m.n]上有意义的两个函数f (x)与g (x).如果对任意x∈[m.n]均有| f (x) – g (x) |≤1.则称f (x)与g (x)在[m.n]上是接近的.否则称f (x)与g (x)在[m.n]上是非接近的.现有两个函数f 1(x) = loga(x – 3a)与f 2 (x) = loga(a > 0.a≠1).给定区间[a + 2.a + 3]． (1)若f 1(x)与f 2 (x)在给定区间[a + 2.a + 3]上都有意义.求a的取值范围, (2)讨论f 1(x)与f 2 (x)在给定区间[a + 2.a + 3]上是否是接近的? (文)已知函数f (x) = ax2 + bx + c (a > b > c)的图像上有两点A (m1.f (m1)).B (m2.f (m2)).满足f (1) = 0且a2 + [f (m1) + f (m2)] · a + f (m1) · f (m2) = 0． (1)求证:b≥0, (2)求证:f (x)的图像被x轴所截得的线段长的取值范围是, (3)问能否得出f (m1 + 3).f (m2 + 3)中至少有一个为正数?请证明你的结论．
网址：http://m.1010jiajiao.com/timu3_id_501325[举报]
（本小题满分14分）已知f(x)=
(x∈R)在区间[－1，1]上是增函数.
（Ⅰ）求实数a的值组成的集合A；
（Ⅱ）设关于x的方程f(x)=
的两个非零实根为x1、x2.试问：是否存在实数m，使得不等式m2+tm+1≥|x1－x2|对任意a∈A及t∈[－1，1]恒成立？若存在，求m的取值范围；若不存在，请说明理由.
（本小题满分14分）
已知幂函数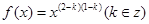
在定义域上递增。
（1）求实数k的值，并写出相应的函数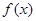
的解析式；
（2）对于（1）中的函数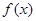，试判断是否存在正数m，使函数
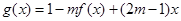，在区间上的最大值为5。若存在，求出m的值；若不存在，请说明理由。
查看习题详情和答案>>
（本小题满分14分）
已知幂函数
在定义域上递增。
（1）求实数k的值，并写出相应的函数
的解析式；
（2）对于（1）中的函数，试判断是否存在正数m，使函数
，在区间上的最大值为5。若存在，求出m的值；若不存在，请说明理由。
在定义域上递增。
的解析式；
，在区间上的最大值为5。若存在，求出m的值；若不存在，请说明理由。
,且
的代数式表示b,并求
的单调区间；
,设函数
处取得极值，记点M (
,
)，N(
,
)，P(
), 
,请仔细观察曲线
(
)，线段MP与曲线f(x)均有异于M,P的公共点，试确定t的最小值，并证明你的结论；
n< m,使得线段PQ与曲线f(x)有异于P、Q的公共点，请直接写出m的取值范围（不必给出求解过程）