Question

（05年湖南卷文）（14分）

设，点P（，0）是函数的图象的一个公共点，两函数的图象在点P处有相同的切线.

（Ⅰ）用表示a，b，c；

（Ⅱ）若函数在（－1，3）上单调递减，求的取值范围.

Answer 1

解析：（I）因为函数，的图象都过点（，0），所以，

     即.因为所以.

      

       又因为，在点（，0）处有相同的切线，所以

       而

       将代入上式得  因此故，，

（II）解法一.

当时，函数单调递减.

由，若；若

由题意，函数在（－1，3）上单调递减，则

所以

又当时，函数在（－1，3）上单调递减.

所以的取值范围为

解法二：

       因为函数在（－1，3）上单调递减，且是（－1，3）

上的抛物线，

       所以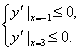  即解得

       所以的取值范围为