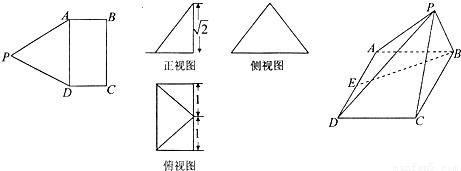
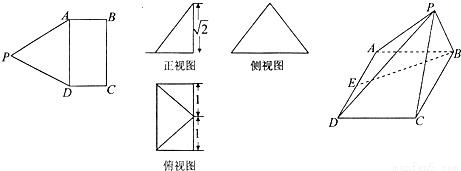
摘要： 如图.矩形ABCD与ADQP所在平面垂直.将矩形ADQP沿PD对折.使得翻折后点Q落在BC上.设AB=1.PA=h.AD=y. (1)试求y关于h的函数解析式, (2)当y取最小值时.指出点Q的位置.并求出此时AD与平面PDQ所成的角, 下.求三棱锥P-ADQ内切球的半径.
网址：http://m.1010jiajiao.com/timu3_id_501170[举报]
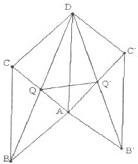如图，矩形ABCD与矩形AB′C′D全等，且所在平面所成的二面角为a，记两个矩形对角线的交点分别为Q，Q′，AB=a，AD=b．（1）求证：QQ′∥平面ABB′；
（2）当b=
| 2 |
| π |
| 3 |
（3）当a＞b，且AC⊥DB'时，求二面角a的余弦值（用a，b表示）． 查看习题详情和答案>>
如图，矩形ABCD与正三角形APD中，AD=2，DC=1，E为AD的中点，现将正三角形APD沿AD折起，得到四棱锥P-ABCD，该四棱锥的三视图如下：
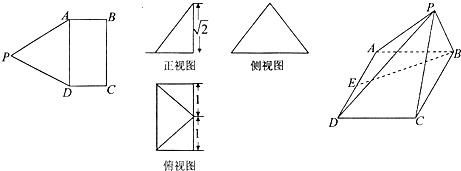
（I）求四棱锥P-ABCD的体积；
（Ⅱ）求异面直线BE，PD所成角的大小；
（Ⅲ）求二面角A-PD-C的正弦值． 查看习题详情和答案>>
（I）求四棱锥P-ABCD的体积；
（Ⅱ）求异面直线BE，PD所成角的大小；
（Ⅲ）求二面角A-PD-C的正弦值． 查看习题详情和答案>>
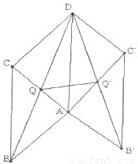如图，矩形ABCD与矩形AB′C′D全等，且所在平面所成的二面角为a，记两个矩形对角线的交点分别为Q，Q′，AB=a，AD=b．（1）求证：QQ′∥平面ABB′；
（2）当
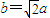，且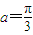
时，求异面直线AC与DB′所成的角；（3）当a＞b，且AC⊥DB'时，求二面角a的余弦值（用a，b表示）．
查看习题详情和答案>>
