摘要：19． 已知数列{an}的前n项和 (1)求数列{an}和{bn}的通项, (2)求证存在自然数n0,对一切不小n0的自然数n.恒有an>5bn. (文)如图所示:四棱锥P-ABCD底面一直角梯形.BA⊥AD.CD⊥AD. CD=2AB.PA⊥底面ABCD.E为PC的中点. (1)证明:EB∥平面PAD, (2)若PA=AD.证明:BE⊥平面PDC, (3)当PA=AD=DC时.求二面角E-BD-C的正切值.
网址：http://m.1010jiajiao.com/timu3_id_501064[举报]
(本小题满分12分)
已知数列{an}的前三项与数列{bn}的前三项对应相等，且a1＋2a2＋22a3＋…＋2n－1an＝8n对任意的n∈N*都成立，数列{bn＋1－bn}是等差数列.
(1)求数列{an}与{bn}的通项公式；
(2)是否存在k∈N*，使得bk－ak∈(0,1)？请说明理由.
(本小题满分12分)
已知数列{an}的前三项与数列{bn}的前三项对应相等，且a1＋2a2＋22a3＋…＋2n－1an＝8n对任意的n∈N*都成立，数列{bn＋1－bn}是等差数列.
(1)求数列{an}与{bn}的通项公式；
(2)是否存在k∈N*，使得bk－ak∈(0,1)？请说明理由.
已知数列{an}的前三项与数列{bn}的前三项对应相等，且a1＋2a2＋22a3＋…＋2n－1an＝8n对任意的n∈N*都成立，数列{bn＋1－bn}是等差数列.
(1)求数列{an}与{bn}的通项公式；
(2)是否存在k∈N*，使得bk－ak∈(0,1)？请说明理由.
（本小题满分12分）
（理科）若
，且当
时，不等式
恒成立，求实数
的取值范围。
（文科）已知数列 {2 n•an} 的前 n 项和 Sn = 9－6n.
(I) 求数列 {an} 的通项公式；
(II) 设 bn = n·(2－log 2 )，求数列 { } 的前 n 项和Tn 。
查看习题详情和答案>>
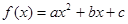，且f(0)=8及f(x+1)－f(x)＝－2x+1。
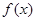的解析式；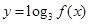
的单调递减区间及值域．
.
}是等差数列；