摘要:21. 椭圆的中心在坐标原点O,右焦点F(c,0)到相应准线的距离为1.倾斜角为45°的直线交椭圆于A.B两点.设AB中点为M.直线AB与OM的夹角为a. (1)用半焦距c表示椭圆的方程及tg; (2)若2<tg<3.求椭圆率心率e的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_501035[举报]
本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
已知以原点![]() 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为![]() ,离心率
,离心率![]() ,
,![]() 是椭圆上的动点.
是椭圆上的动点.
(Ⅰ)若![]() 的坐标分别是
的坐标分别是![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅱ)如题(20)图,点![]() 的坐标为
的坐标为![]() ,
,![]() 是圆
是圆![]() 上的点,
上的点,![]() 是点
是点![]() 在
在![]() 轴上的射影,点
轴上的射影,点![]() 满足条件:
满足条件:![]() ,
,![]() .求线段
.求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;

(本小题满分12分)
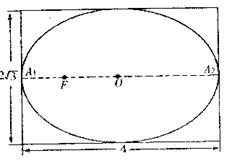
有一幅椭圆型彗星轨道图,长4cm,高![]() ,如下图,
,如下图,
已知O为椭圆中心,A1,A2是长轴两端点,
|
(Ⅰ)建立适当的坐标系,写出椭圆方程,
并求出当彗星运行到太阳正上方时二者在图上的距离;
(Ⅱ)直线l垂直于A1A2的延长线于D点,|OD|=4,
设P是l上异于D点的任意一点,直线A1P,A2P分别
交椭圆于M、N(不同于A1,A2)两点,问点A2能否
在以MN为直径的圆上?试说明理由.
查看习题详情和答案>> (本小题满分12分)已知中心在原点的椭圆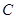 的离心率
的离心率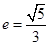 ,一条准线方程为
,一条准线方程为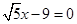
(1)求椭圆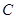 的标准方程;
的标准方程;
(2)若以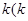 >0)为斜率的直线
>0)为斜率的直线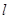 与椭圆
与椭圆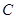 相交于两个不同的点
相交于两个不同的点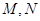 ,且线段
,且线段 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为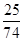 ,求
,求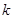 的取值范围。
的取值范围。
查看习题详情和答案>>
 、
、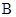 、
、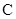 是椭圆
是椭圆 :
: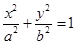 (
(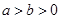 )上的三点,其中点
)上的三点,其中点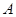 的坐标为
的坐标为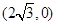 ,
,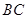 过椭圆的中心,且
过椭圆的中心,且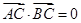 ,
,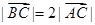 。
。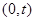 的直线
的直线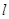 (斜率存在时)与椭圆
(斜率存在时)与椭圆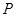 ,
,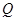 ,设
,设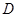 为椭圆
为椭圆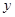 轴负半轴的交点,且
轴负半轴的交点,且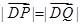 ,求实数
,求实数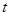 的取值范围.
的取值范围. (
( )的右焦点为
)的右焦点为 ,离心率为
,离心率为 .
. ,求椭圆的方程;
,求椭圆的方程; 与椭圆相交于
与椭圆相交于 ,
, 两点,
两点, 分别为线段
分别为线段 的中点. 若坐标原点
的中点. 若坐标原点 在以
在以 为直径的圆上,且
为直径的圆上,且 ,求
,求 的取值范围.
的取值范围.