题目内容
(本小题满分12分)已知中心在原点的椭圆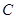 的离心率
的离心率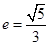 ,一条准线方程为
,一条准线方程为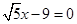
(1)求椭圆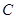 的标准方程;
的标准方程;
(2)若以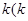 >0)为斜率的直线
>0)为斜率的直线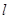 与椭圆
与椭圆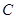 相交于两个不同的点
相交于两个不同的点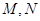 ,且线段
,且线段 的垂直平分线与两坐标轴围成的三角形的面积为
的垂直平分线与两坐标轴围成的三角形的面积为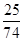 ,求
,求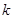 的取值范围。
的取值范围。
【答案】
(1)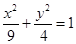 ;(2)
;(2)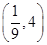
【解析】
试题分析:(1)因为椭圆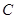 的离心率
的离心率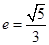 ,一条准线方程为
,一条准线方程为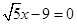 .应用待定系数求得椭圆的标准方程.
.应用待定系数求得椭圆的标准方程.
(2)假设直线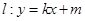 (
(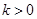 )方程.其中有两个参数
)方程.其中有两个参数 .联立椭圆方程.消去
.联立椭圆方程.消去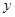 即可得一个关于
即可得一个关于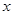 的二次方程.首先由二次方程根的判别式大于零可得一个关于
的二次方程.首先由二次方程根的判别式大于零可得一个关于 的不等的关系式.其次由韦达定理写出两个根与
的不等的关系式.其次由韦达定理写出两个根与 的关系式.写出线段
的关系式.写出线段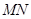 的中垂线的方程.从而可得中垂线与两坐标轴的截距.再写出垂直平分线与两坐标轴围成的三角形的面积,依题意即可得一个关于
的中垂线的方程.从而可得中垂线与两坐标轴的截距.再写出垂直平分线与两坐标轴围成的三角形的面积,依题意即可得一个关于 的等式.由这两步消去
的等式.由这两步消去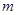 .即可得
.即可得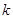 的取值范围.
的取值范围.
试题解析:(1)由已知设椭圆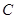 的标准方程为,
的标准方程为,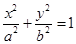
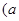 >
>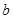 >0)
>0)
由题设得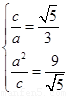 解得
解得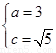 ,
,

所以椭圆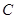 的标准方程为
的标准方程为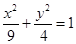 4分
4分
(2)由题意设直线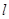 的方程为
的方程为 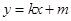 (
(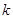 >0)
>0)
由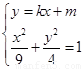 消去
消去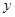 得
得 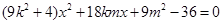 ①
①
设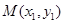
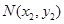 则
则 ,
, =
=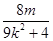
线段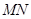 的中点坐标
的中点坐标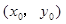 满足
满足
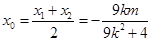
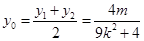
从而线段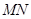 的垂直平分线的方程为
的垂直平分线的方程为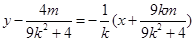
此直线与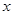 轴,
轴,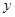 轴的交点坐标分别为
轴的交点坐标分别为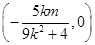 、
、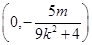
由题设可得 整理得
整理得 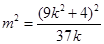 (
(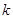 >0) ②
>0) ②
由题意在①中有 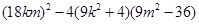 >0 整理得
>0 整理得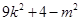 >0
>0
将②代入得 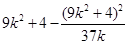 >0 (
>0 (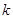 >0),
>0),
即 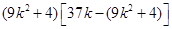 >0,
>0, 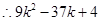 <0,即
<0,即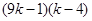 <0
<0
∴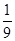 <
<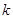 <4 所以
<4 所以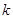 的取值范围是
的取值范围是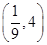 。 12分
。 12分
考点:1.待定系数求椭圆的方程.2.直线与椭圆的位置关系.3.线段的垂直平分线.4.方程与不等式转化的思想.

练习册系列答案
相关题目