摘要: 已知F, F, 点P满足||+||=4. (1) 写出点P的轨迹C的方程; (2) 曲线C上点M满足: |MF|=d+1, d表示M点到曲线C的左准线的距离, 过点F的直线l 交曲线C于A.B两点, 且△ABF被x轴分成的两个三角形面积比=(≤≤3), 求直线l 的倾斜角的取值范围.
网址:http://m.1010jiajiao.com/timu3_id_500436[举报]
(本小题12分)
已知函数f(x)= x
x -(2a+1)x
-(2a+1)x +3a(a+2)x+
+3a(a+2)x+ ,其中a为实数。
,其中a为实数。
(1)当a=-1时,求函数y=f(x)在[0,6]上的最大值与最小值;
(2)当函数y=f (x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。
(x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。
查看习题详情和答案>>
(本小题12分)
已知函数f(x)=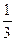 x
x -(2a+1)
-(2a+1) x
x +3a(a+2)x+
+3a(a+2)x+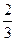 ,其中a为实数。
,其中a为实数。
(1)当a=-1时,求函数y=f(x)在[0,6]上的最大值与最小值;
(2)当函数y=f (x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。
(x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。
(本小题12分)已知函数f(x)=ax3+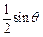 x2-2x+c,过点
x2-2x+c,过点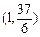 ,且在(-2,1)内单调递减,在[1,
,且在(-2,1)内单调递减,在[1,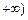 上单调递增。
上单调递增。
(1)证明sinθ=1,并求f(x)的解析式。
(2)若对于任意的x1,x2∈[m,m+3](m≥0),不等式|f(x1)-f(x2)|≤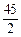 恒成立。试问这样的m是否存在,若存在,请求出m的范围,若不存在,说明理由。
恒成立。试问这样的m是否存在,若存在,请求出m的范围,若不存在,说明理由。
(3)已知数列{an}中,a1∈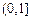 ,an+1=f(an),求证:an+1>8·lnan(n∈N*)。
,an+1=f(an),求证:an+1>8·lnan(n∈N*)。
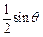 x2-2x+c,过点
x2-2x+c,过点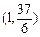 ,且在(-2,1)内单调递减,在[1,
,且在(-2,1)内单调递减,在[1,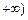 上单调递增。
上单调递增。(1)证明sinθ=1,并求f(x)的解析式。
(2)若对于任意的x1,x2∈[m,m+3](m≥0),不等式|f(x1)-f(x2)|≤
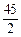 恒成立。试问这样的m是否存在,若存在,请求出m的范围,若不存在,说明理由。
恒成立。试问这样的m是否存在,若存在,请求出m的范围,若不存在,说明理由。(3)已知数列{an}中,a1∈
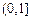 ,an+1=f(an),求证:an+1>8·lnan(n∈N*)。
,an+1=f(an),求证:an+1>8·lnan(n∈N*)。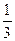 x
x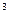 -(2a+1)
-(2a+1) x
x +3a(a+2)x+
+3a(a+2)x+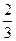 ,其中a为实数。
,其中a为实数。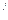 (x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。
(x)的图像在(0,6)上与x轴有唯一的公共点时,求实数a的取值范围。