摘要:17.解:⑴由题意知:. 设函数图象上的任意一点关于原点的对称点为P(x,y),则 .因为点 ⑵ 连续. 即.由上为减函数.当 时取最小值0.故 另解:. .解得
网址:http://m.1010jiajiao.com/timu3_id_500388[举报]
(本题满分16分)设函数y=f(x)对任意实数x,都有f(x)=2f(x+1),当x∈[0,1]时,f(x)=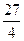 x2(1-x).
x2(1-x).
(Ⅰ)已知n∈N+,当x∈[n,n+1]时,求y=f(x)的解析式;
(Ⅱ)求证:对于任意的n∈N+,当x∈[n,n+1]时,都有|f(x)|≤ ;
;
(Ⅲ)对于函数y=f(x) (x∈[0,+∞
(x∈[0,+∞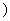 ,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
(本题满分16分)设函数y=f(x)对任意实数x,都有f(x)=2f(x+1),当x∈[0,1]时,f(x)= x2(1-x).
x2(1-x).
(Ⅰ)已知n∈N+,当x∈[n,n+1]时,求y=f(x)的解析式;
(Ⅱ)求证:对于任意的n∈N+,当x∈[n,n+1]时,都有|f(x)|≤ ;
;
(Ⅲ)对于函数y=f(x)(x∈[0,+∞ ,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
查看习题详情和答案>>
(本题满分16分)设函数y=f(x)对任意实数x,都有f(x)=2f(x+1),当x∈[0,1]时,f(x)=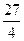 x2(1-x).
x2(1-x).
(Ⅰ)已知n∈N+,当x∈[n,n+1]时,求y=f(x)的解析式;
(Ⅱ)求证:对于任意的n∈N+,当x∈[n,n+1]时,都有|f(x)|≤ ;
;
(Ⅲ)对于函数y=f(x) (x∈[0,+∞
(x∈[0,+∞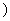 ,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
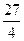 x2(1-x).
x2(1-x). (Ⅰ)已知n∈N+,当x∈[n,n+1]时,求y=f(x)的解析式;
(Ⅱ)求证:对于任意的n∈N+,当x∈[n,n+1]时,都有|f(x)|≤
 ;
;(Ⅲ)对于函数y=f(x)
 (x∈[0,+∞
(x∈[0,+∞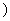 ,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由 对任意的实数
对任意的实数 ,都有
,都有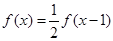 ,且当
,且当 时,
时, 。
。 时,求
时,求 ,试问:在它的图象上是否存在点
,试问:在它的图象上是否存在点 ,使得函数在点
,使得函数在点 平行。若存在,那么这样的点
平行。若存在,那么这样的点 ,且
,且  ,记
,记 ,求证:
,求证:  。
。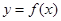 对任意的实数
对任意的实数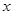 ,都有
,都有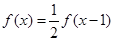 ,且当
,且当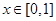 时,
时,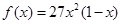 。
。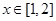 时,求
时,求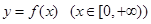 ,试问:在它的图象上是否存在点
,试问:在它的图象上是否存在点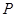 ,使得函数在点
,使得函数在点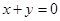 平行。若存在,那么这样的点
平行。若存在,那么这样的点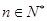 ,且
,且 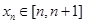 ,记
,记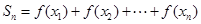 ,求证:
,求证: 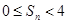 。
。