题目内容
(本题满分16分)设函数y=f(x)对任意实数x,都有f(x)=2f(x+1),当x∈[0,1]时,f(x)=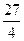 x2(1-x).
x2(1-x).
(Ⅰ)已知n∈N+,当x∈[n,n+1]时,求y=f(x)的解析式;
(Ⅱ)求证:对于任意的n∈N+,当x∈[n,n+1]时,都有|f(x)|≤ ;
;
(Ⅲ)对于函数y=f(x) (x∈[0,+∞
(x∈[0,+∞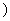 ,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
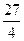 x2(1-x).
x2(1-x). (Ⅰ)已知n∈N+,当x∈[n,n+1]时,求y=f(x)的解析式;
(Ⅱ)求证:对于任意的n∈N+,当x∈[n,n+1]时,都有|f(x)|≤
 ;
;(Ⅲ)对于函数y=f(x)
 (x∈[0,+∞
(x∈[0,+∞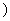 ,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由
,若在它的图象上存在点P,使经过点P的切线与直线x+y=1平行,那么这样点有多少个?并说明理由解:(Ⅰ)由f(x)=2f(x+1)→f(x)=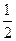 (x-1),x∈[n,n+1],则(x-n)∈[0,1]
(x-1),x∈[n,n+1],则(x-n)∈[0,1]
→f(x-n)=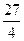 (x-n)2(1+n-x). f(x)=
(x-n)2(1+n-x). f(x)=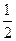 f(x-1)=
f(x-1)=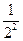 f(x-2)=…=
f(x-2)=…= f(x-n)=
f(x-n)=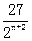 (x-n)2(1+n-x). (n=0也适用). ………………4分
(x-n)2(1+n-x). (n=0也适用). ………………4分
(Ⅱ)f
 (x)=
(x)=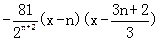 ,由f
,由f (x)=0得x=n或x=n+
(x)=0得x=n或x=n+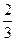
f(x)的极大值为f(x)的最大值,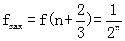 ,
,
又f(x)≥f(n)=f(n+1)=0,∴|f(x)|=f(x)≤ (x∈[n,n+1]).…8分
(x∈[n,n+1]).…8分
(Ⅲ)y=f(x),x∈[0,+∞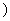 即为y=f(x),x∈[n,n+1],f
即为y=f(x),x∈[n,n+1],f (x)="-1."
(x)="-1."
本题转化为方程f
 (x)=-1在[n,n+1]上有解问题
(x)=-1在[n,n+1]上有解问题
即方程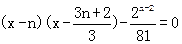 在[n,n+1]内是否有解. ……11分
在[n,n+1]内是否有解. ……11分
令g(x)=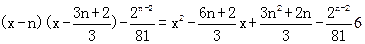 ,
,
对轴称x=n +
+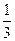 ∈[n,n+1],
∈[n,n+1],
又△=…=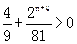 ,g(n)=
,g(n)=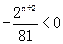 ,g(n+1)=
,g(n+1)=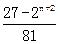 ,
,
①当0≤n≤2时,g(n+1)≥0,∴方程g(x)=0在区间[0,1],[1,2],[2,3]上分别有一解,即存在三个点P;
②n≥3时,g(n+1)<0,方程g(x)=0在[n,n+1]上无解,即不存在这样点P.
综上所述:满足条件的点P有三个. …………………………16分
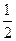 (x-1),x∈[n,n+1],则(x-n)∈[0,1]
(x-1),x∈[n,n+1],则(x-n)∈[0,1]→f(x-n)=
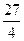 (x-n)2(1+n-x). f(x)=
(x-n)2(1+n-x). f(x)=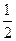 f(x-1)=
f(x-1)=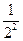 f(x-2)=…=
f(x-2)=…= f(x-n)=
f(x-n)=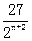 (x-n)2(1+n-x). (n=0也适用). ………………4分
(x-n)2(1+n-x). (n=0也适用). ………………4分(Ⅱ)f

 (x)=
(x)=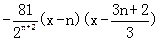 ,由f
,由f (x)=0得x=n或x=n+
(x)=0得x=n或x=n+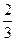
| x | n | (n,n+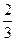 ) ) | n+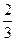 | (n+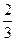 ,n+1) ,n+1) | n+1 |
f (x) (x) | | + | 0 | - | + |
| | 0 | ↗ | 极大 | ↘ | 0 |
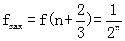 ,
,又f(x)≥f(n)=f(n+1)=0,∴|f(x)|=f(x)≤
 (x∈[n,n+1]).…8分
(x∈[n,n+1]).…8分(Ⅲ)y=f(x),x∈[0,+∞
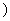 即为y=f(x),x∈[n,n+1],f
即为y=f(x),x∈[n,n+1],f (x)="-1."
(x)="-1." 本题转化为方程f

 (x)=-1在[n,n+1]上有解问题
(x)=-1在[n,n+1]上有解问题即方程
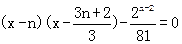 在[n,n+1]内是否有解. ……11分
在[n,n+1]内是否有解. ……11分令g(x)=
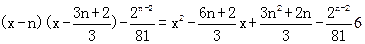 ,
,对轴称x=n
 +
+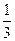 ∈[n,n+1],
∈[n,n+1],
又△=…=
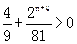 ,g(n)=
,g(n)=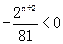 ,g(n+1)=
,g(n+1)=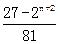 ,
,①当0≤n≤2时,g(n+1)≥0,∴方程g(x)=0在区间[0,1],[1,2],[2,3]上分别有一解,即存在三个点P;
②n≥3时,g(n+1)<0,方程g(x)=0在[n,n+1]上无解,即不存在这样点P.
综上所述:满足条件的点P有三个. …………………………16分
略

练习册系列答案
相关题目
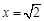 是函数
是函数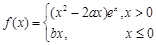 的极值点.当
的极值点.当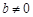 时,讨论函数
时,讨论函数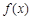 的单调性;
的单调性;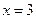 是函数
是函数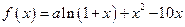 的一个极值点。
的一个极值点。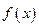 的单调区间;
的单调区间;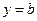 与函数
与函数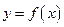 的图象有3个交点,求
的图象有3个交点,求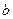 的取值范围。
的取值范围。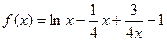 .
.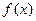 的单调区间;
的单调区间;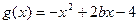 ,若对任意
,若对任意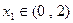 ,
,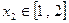 ,不等式
,不等式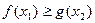 恒成立,求实数
恒成立,求实数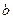 的取值范围
的取值范围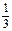 x3+
x3+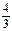 ,则过点P(2
,则过点P(2 ,4)的切线方程是 ( )
,4)的切线方程是 ( ) .
.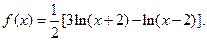
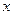 为何值时,
为何值时,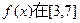 上取得最大值;
上取得最大值;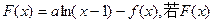 是单调递增函数,求
是单调递增函数,求 的取值范围.
的取值范围.
 即可,不必算出最结果.)
即可,不必算出最结果.) .
.