摘要：根据题设条件的特征进行观察.分析.从而得出正确的结论. [例4] 设含有10个元素的集合全部子集数为.其中由3个元素组成的子集数为.则的值为 . 解:由..故. [类比1] 设是首项为1的正项数列.且, 则它们的通项公式是 . [类比2] 如右图.在直四棱柱 中.当底面四边形满足条件 时.有(填上你认为正确的一个条件 即可.不必考虑所有可能性的情形). [类比3] 椭圆长轴上一个顶点为 A. 以A为直角顶点作一个内接于椭圆的等腰直角 三角形.该三角形的面积是 . [类比4] 已知函数.给出下列命题: ①必是偶函数, ②时.的图象必关于直线对称, ③若.则在区间上是增函数, ④有最大值. 其中正确的命题的序号是 .
网址：http://m.1010jiajiao.com/timu3_id_500320[举报]
某种商品在30天内每件的销售价格P（元）与时间t（天）的函数关系用如图所示的两条直线段表示：又该商品在30天内日销售量Q（件）与时间t（天）之间的关系如下表所示：
| 第t天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
（2），试问30天中第几天日销售金额最大？最大金额为多少元？（日销售金额=每件的销售价格×日销售量）． 查看习题详情和答案>>
某种商品在30天内每件的销售价格P（元）与时间t（天） 的函数
关系用如图所示的两条直线段表示：
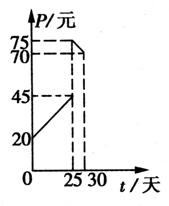又该商品在30天内日销售量Q（件）与时间t（天）之间的关系
如下表所示：
| 第t天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 |
|
10（1）根据题设条件，写出该商品每件的销售价格P与时间t的函
数关系式；并确定日销售量Q与时间t的一个函数关系式；
（2），试问30天中第几天日销售金额最大？最大金额为多少元？
（日销售金额=每件的销售价格×日销售量）.
查看习题详情和答案>>
某种商品在30天内每件的销售价格P（元）与时间t（天）的函数关系用如图所示的两条直线段表示：
又该商品在30天内日销售量Q（件）与时间t（天）之间的关系如下表所示：
（1）根据题设条件，写出该商品每件的销售价格P与时间t的函数关系式；并确定日销售量Q与时间t的一个函数关系式；
（2），试问30天中第几天日销售金额最大？最大金额为多少元？（日销售金额=每件的销售价格×日销售量）．
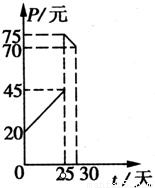查看习题详情和答案>>
又该商品在30天内日销售量Q（件）与时间t（天）之间的关系如下表所示：
| 第t天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
（2），试问30天中第几天日销售金额最大？最大金额为多少元？（日销售金额=每件的销售价格×日销售量）．
查看习题详情和答案>>
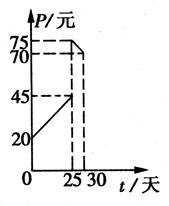
10