摘要：根据题设条件与结论的特殊性.构造出一些新的数学形式.并借助于它认识和解决问题的一种方法. [例3] 4个不同的小球放入编号为1.2.3.4的4个盒中.则只有1个空盒的放法共有 种. 解:符合条件的放法是:有一个盒中放2个球.有2个盒中各放1个球.因此可先将球 分成3堆(一堆2个.其余2堆各1个.即构造了球的“堆 ).然后从4个盒中选出3个盒 放1堆球.依分步计算原理.符合条件的放法有(种). [类比1] 在球面上有四个点P.A.B.C.如果PA.PB.PC两两互相垂直.且PA=PB= PC=.那么这个球面面积是 .
网址：http://m.1010jiajiao.com/timu3_id_500319[举报]
某种商品在30天内每件的销售价格P（元）与时间t（天）的函数关系用如图所示的两条直线段表示：又该商品在30天内日销售量Q（件）与时间t（天）之间的关系如下表所示：
| 第t天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
（2），试问30天中第几天日销售金额最大？最大金额为多少元？（日销售金额=每件的销售价格×日销售量）． 查看习题详情和答案>>
某种商品在30天内每件的销售价格P（元）与时间t（天） 的函数
关系用如图所示的两条直线段表示：
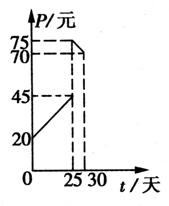又该商品在30天内日销售量Q（件）与时间t（天）之间的关系
如下表所示：
| 第t天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 |
|
10（1）根据题设条件，写出该商品每件的销售价格P与时间t的函
数关系式；并确定日销售量Q与时间t的一个函数关系式；
（2），试问30天中第几天日销售金额最大？最大金额为多少元？
（日销售金额=每件的销售价格×日销售量）.
查看习题详情和答案>>某种商品在30天内每件的销售价格P（元）与时间t（天） 的函数
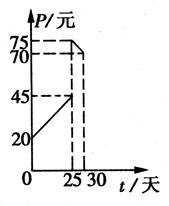
关系用如图所示的两条直线段表示：
又该商品在30天内日销售量Q（件）与时间t（天）之间的关系
如下表所示：
（1）根据题设条件，写出该商品每件的销售价格P与时间t的函
数关系式；并确定日销售量Q与时间t的一个函数关系式；
（2），试问30天中第几天日销售金额最大？最大金额为多少元？
（日销售金额=每件的销售价格×日销售量）.
关系用如图所示的两条直线段表示：
又该商品在30天内日销售量Q（件）与时间t（天）之间的关系
如下表所示：
| 第t天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 |  10 |
数关系式；并确定日销售量Q与时间t的一个函数关系式；
（2），试问30天中第几天日销售金额最大？最大金额为多少元？
（日销售金额=每件的销售价格×日销售量）.
某种商品在30天内每件的销售价格P（元）与时间t（天）的函数关系用如图所示的两条直线段表示：
又该商品在30天内日销售量Q（件）与时间t（天）之间的关系如下表所示：
（1）根据题设条件，写出该商品每件的销售价格P与时间t的函数关系式；并确定日销售量Q与时间t的一个函数关系式；
（2），试问30天中第几天日销售金额最大？最大金额为多少元？（日销售金额=每件的销售价格×日销售量）．
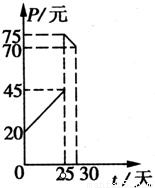查看习题详情和答案>>
又该商品在30天内日销售量Q（件）与时间t（天）之间的关系如下表所示：
| 第t天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
（2），试问30天中第几天日销售金额最大？最大金额为多少元？（日销售金额=每件的销售价格×日销售量）．
查看习题详情和答案>>
