摘要：12．(1)由题意.有x2-2mx+2m2+＞0对任意的x∈R恒成立 所以△＝4m2-4(2m2+)＜0 即-m2-＜0 ∴＞0 由于分子恒大于0.只需m2-3＞0即可 所以m＜-或m＞ ∴M＝{m|m＜-或m＞} --4分 (2)x2-2mx+2m2+＝(x-m)2+m2+≥m2+ 当且仅当x＝m时等号成立. 所以.题设对数函数的真数的最小值为m2+ --7分 又因为以3为底的对数函数为增函数 ∴f(x)≥log3(m2+) ∴当且仅当x＝m(m∈M)时.f(x)有最小值为log3(m2+) --10分 又当m∈M时.m2-3＞0 ∴m2+＝m2-3++3≥2+3＝9 当且仅当m2-3＝.即m＝±时. log3(m2+)有最小值log3(6+)＝log39＝2 ∴当x＝m＝±时.其函数有最小值2.
网址：http://m.1010jiajiao.com/timu3_id_500035[举报]
设椭圆
的左、右顶点分别为
，点
在椭圆上且异于两点，
为坐标原点.
（Ⅰ）若直线
与
的斜率之积为
，求椭圆的离心率；
（Ⅱ）若
，证明直线
的斜率
满足
【解析】(1)解：设点P的坐标为
.由题意，有
①
由
，得
，
由
，可得
，代入①并整理得
由于
，故
.于是
，所以椭圆的离心率
（2）证明：（方法一）
依题意，直线OP的方程为
，设点P的坐标为.
由条件得
消去
并整理得
②
由
，
及
，
得
.
整理得
.而
，于是
，代入②，
整理得
由
，故
，因此
.
所以
.
(方法二)
依题意，直线OP的方程为，设点P的坐标为.
由P在椭圆上，有
因为，
，所以
，即
③
由，，得整理得.
于是，代入③，
整理得
解得，
所以.
查看习题详情和答案>>
如图，
，
，…，
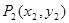，…是曲线
上的点，
，
，…，
，…是
轴正半轴上的点，且
，
，…，
，…
均为斜边在轴上的等腰直角三角形（
为坐标原点）．
（1）写出
、
和
之间的等量关系，以及、和
之间的等量关系；
（2）求证：
（
）；
（3）设
，对所有，
恒成立，求实数
的取值范围．
【解析】第一问利用有
，
得到
第二问证明：①当
时，可求得
，命题成立；②假设当
时，命题成立，即有
则当
时，由归纳假设及
，
得
第三问
．………………………2分
因为函数
在区间
上单调递增，所以当时，
最大为
，即
解：（1）依题意，有，，………………4分
（2）证明：①当时，可求得，命题成立；
……………2分
②假设当时，命题成立，即有，……………………1分
则当时，由归纳假设及，
得．
即
解得
（
不合题意，舍去）
即当时，命题成立． …………………………………………4分
综上所述，对所有，． ……………………………1分
（3） 
．………………………2分
因为函数在区间上单调递增，所以当时，最大为，即
．……………2分
由题意，有
．
所以，
查看习题详情和答案>>