摘要:解:(1)设动点的坐标为P,,= = ∴·== 由题意得∣PH∣2=2·· 即 即.所求点P的轨迹为椭圆 关于直线x+y=1的对称点E.则∣QE∣=∣QN∣ 双曲线的C实轴长2a=(当且仅当Q.E.M共线时取“= ).此时.实轴长2a最大为 所以.双曲线C的实半轴长a= 又 ∴双曲线C的方程式为
网址:http://m.1010jiajiao.com/timu3_id_500031[举报]
设动点![]() 的坐标为
的坐标为![]() (x、
(x、![]() ),且动点
),且动点![]() 到定点
到定点![]() ,
,![]() 的距离之和为8.
的距离之和为8.
(I)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() (
(![]() 为坐标原点),是否存在直线
为坐标原点),是否存在直线![]() ,使得四边形
,使得四边形![]() 为矩形,若存在,求出直线
为矩形,若存在,求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
设动点![]() 的坐标为
的坐标为![]() (x、
(x、![]() ),向量
),向量![]()
![]() ,
,![]()
![]() ,且
,且![]() =8.
=8.
(I)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() (
(![]() 为坐标原点),是否存在直线
为坐标原点),是否存在直线![]() ,使得四边形
,使得四边形![]() 为矩形,若存在,求出直线
为矩形,若存在,求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
已知圆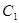 的圆心在坐标原点
的圆心在坐标原点 ,且恰好与直线
,且恰好与直线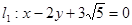 相切,设点A为圆上一动点,
相切,设点A为圆上一动点,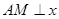 轴于点
轴于点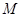 ,且动点
,且动点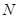 满足
满足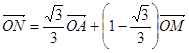 ,设动点
,设动点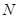 的轨迹为曲线
的轨迹为曲线
(1)求曲线C的方程,
(2)直线l与直线l,垂直且与曲线C交于B、D两点,求△OBD面积的最大值.
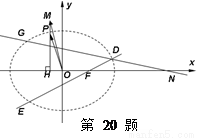
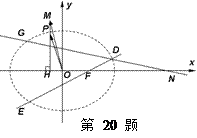
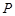 是椭圆
是椭圆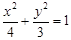 上一动点,点
上一动点,点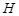 是点
是点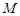 在
在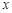 轴上的射影,坐标平面
轴上的射影,坐标平面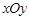 内动点
内动点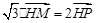 (
(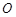 为坐标原点),设动点
为坐标原点),设动点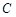 .
.
 的直线
的直线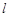 交曲线
交曲线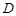 ,
,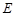 两点,且
两点,且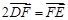 ,点
,点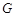 ,求直线
,求直线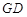 的方程.
的方程.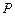 是椭圆
是椭圆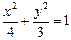 上一动点,点
上一动点,点 是点
是点 在
在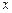 轴上的射影,坐标平面
轴上的射影,坐标平面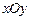 内动点
内动点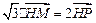 (
( 为坐标原点),设动点
为坐标原点),设动点 .
.
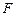 的直线
的直线 交曲线
交曲线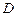 ,
,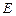 两点,且
两点,且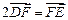 ,点
,点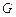 ,求直线
,求直线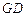 的方程.
的方程.