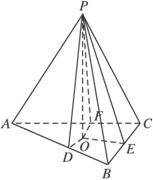
摘要：三棱锥P-ABC中.三侧棱PA.PB.PC两两相互垂直.三侧面面积分别为S1.S2.S3.底面积为S.三侧面与底面分别成角α.β.γ.(1)求S(用S1.S2.S3表示),(2)求证:cos2α+cos2β+cos2γ=1, 解:设PA=a.PB=b.PC=c.则S1=ab .S2=bc.S3=ca. 作PD⊥BC于D.连AD.易证BC⊥平面PAD. 于是BC⊥AD,S△ABC=BC×AD.在Rt△APD中.AD2=a2+PD2. 在Rt△BPC中.PD2=. ∴AD2=a2+ ∴S△ABC2=(BC×AD)2=(a2b2+b2c2+c2a2)= ∴ 证明:由(1)知.PD⊥BC.AD⊥BC.∴∠PDA是侧面PBC与底面ABC所成二面角的平面角.不妨设∠PDA=α. PD2=.AD2= ∴cos2α=,同理cos2β=, cos2γ= ,∴cos2α+cos2β+cos2γ=1

网址：http://m.1010jiajiao.com/timu3_id_499377[举报]