题目内容

三棱锥P-ABC中，三侧棱PA、PB、PC两两相互垂直，三侧面面积分

别为S1、S2、S3，底面积为S，三侧面与底面分别成角α、β、γ，（1）求S（用S1、S2、S3表示）；（2）求证：cos2α+cos2β+cos2γ=1；

见解析


解析:

设PA=a，PB=b，PC=c，则S1=ab ，S2=bc，S3=ca，

作PD⊥BC于D，连AD，

易证BC⊥平面PAD，

于是BC⊥AD；

S△ABC=BC×AD，

在Rt△APD中，AD2=a2+PD2，

在Rt△BPC中，PD2=，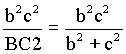

∴AD2=a2+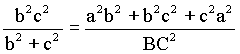

∴S△ABC2=（BC×AD）2=（a2b2+b2c2+c2a2）=

∴

证明：由（1）知，PD⊥BC，AD⊥BC，∴∠PDA是侧面PBC与底面ABC所成二面角的平面角，不妨设∠PDA=α，

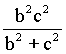PD2=，AD2=

∴cos2α=；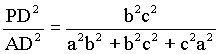

同理cos2β=；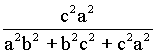

cos2γ= ；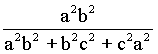

 ∴cos2α+cos2β+cos2γ=1

练习册系列答案
相关题目
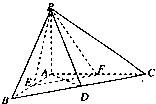精英家教网如图，在三棱锥P-ABC中，△PAB是等边三角形，∠PAC=∠PBC=90°．
（1）证明：AB⊥PC；
（2）若PC=4，且平面PAC⊥平面PBC，求三棱锥P-ABC的体积．
精英家教网如图，在三棱锥P-ABC中，PA⊥平面ABC，∠BAC=
π2
，PA=2，AB=AC=4，点D、E、F分别为BC、AB、AC的中点．
（I）求证：EF⊥平面PAD；
（II）求点A到平面PEF的距离；
（III）求二面角E-PF-A的大小．
精英家教网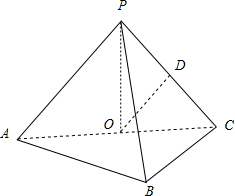如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=kPA，点O、D分别是AC、PC的中点，OP⊥底面ABC．
（Ⅰ）当k=
12
时，求直线PA与平面PBC所成角的大小；
（Ⅱ）当k取何值时，O在平面PBC内的射影恰好为△PBC的重心？
精英家教网如图，在三棱锥P-ABC中，PC⊥平面ABC，△ABC为正三角形，D、E、F分别是BC，PB，CA的中点．
（1）证明平面PBF⊥平面PAC；
（2）判断AE是否平行于平面PFD，并说明理由；
（3）若PC=AB=2，求三棱锥P-DEF的体积．
在正三棱锥P-ABC中，M，N分别是PB，PC的中点，若截面AMN⊥侧面PBC，则此棱锥截面与底面所成的二面角正弦值是
6
6
6
6
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网