题目内容
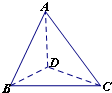
已知正三棱锥A-BCD的底边长为a,E,F分别是AB,BC的中点,且AC⊥DE.

(1)求此正三棱锥的体积V;
(2)求二面角E-FD-B的正弦值.
答案:
解析:
解析:
|
(1)由正三棱锥A-BCD知AC⊥BD ∵AC⊥DE,∴AC⊥平面ABD. ∴∠BAC=∠DAC=∠BAD= ∴AB=AC=AD= V= (2)分别过A、E作平面BCD的垂线,垂足为 连结 ∵EF∥AC,∴EF⊥平面ABD, ∠FED= ∴ 在 设二面角E-FD-B大小为θ, 则cosθ= ∴二面角E-FD-B的正弦值为 |

练习册系列答案
相关题目

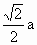 .
. ×
× AB·AC·AD=
AB·AC·AD= .
. 、
、 ,由正三棱锥可知
,由正三棱锥可知 ,
, ,
, 是△EDF在平面BCD内的射影.
是△EDF在平面BCD内的射影. ,EF=
,EF= =
= ,
, ,
,
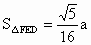 .
. 中,DF=
中,DF= ,
,
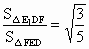 ,sinθ=
,sinθ= .
. 已知正三棱锥A-BCD中,底面边长BC为3,侧棱长AB为
已知正三棱锥A-BCD中,底面边长BC为3,侧棱长AB为

 ,求此正三棱锥的体积及内切球的表面积.
,求此正三棱锥的体积及内切球的表面积.