题目内容
已知正三棱锥A-BCD，E为侧棱AB中点，CE⊥AD，若底面△ABC边长为2，则此三棱锥的体积为（ ）A．
B．
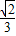
C．
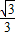
D．
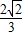
【答案】分析：由已知，CE⊥AD，为两条异面直线垂直，需求另外的线线垂直得出线面垂直关系，便于问题解决，结合正三棱锥的性质，由对棱垂直BC⊥AD可用，由此AD⊥面ABC
解答：解：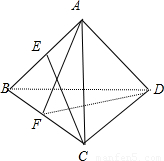
如图．取BC中点F，连接AF，DF可知BC⊥AF，BC⊥DF，
∴BC⊥面AFD，∴BC⊥AD，
由已知CE⊥AD，∴AD⊥面ABC．
所以三条侧棱两两互相垂直．三个侧面均为等腰直角三角形．
底面△ABC边长为2，则AB=AC=AD=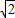
三棱锥的体积V=
=
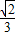
故选B
点评：本题考查锥体体积计算，要确定好底面和高．对于常见几何体的性质，要有较好的认识与掌握．本题利用正三棱锥对棱垂直是关键．
解答：解：
如图．取BC中点F，连接AF，DF可知BC⊥AF，BC⊥DF，
∴BC⊥面AFD，∴BC⊥AD，
由已知CE⊥AD，∴AD⊥面ABC．
所以三条侧棱两两互相垂直．三个侧面均为等腰直角三角形．
底面△ABC边长为2，则AB=AC=AD=
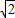
三棱锥的体积V=
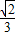
=故选B
点评：本题考查锥体体积计算，要确定好底面和高．对于常见几何体的性质，要有较好的认识与掌握．本题利用正三棱锥对棱垂直是关键．
练习册系列答案
相关题目
已知正三棱锥A-BCD中，底面边长BC为3，侧棱长AB为
，求此正三棱锥的体积及内切球的表面积．