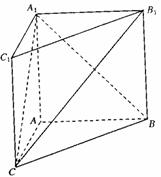
摘要: 如图:已知A1B1C1-ABC是正三棱柱.D是AC中点. Ⅰ.证明:AB1∥平面DBC1, Ⅱ.假设AB1⊥BC1.求以BC1为棱DBC1与CBC1为面的二面角α的度数.
网址:http://m.1010jiajiao.com/timu3_id_499050[举报]
(本小题满分12分)
如图1,已知四边形ABCD是上、下底长分别为2和6,高DO为![]() 的等腰梯形,将它沿DO折成
的等腰梯形,将它沿DO折成![]() 的二面角A-DO-B,如图2,连结AB,AC,BD,OC.
的二面角A-DO-B,如图2,连结AB,AC,BD,OC.
 (Ⅰ)求三棱锥A-BOD的体积V;
(Ⅰ)求三棱锥A-BOD的体积V;
(Ⅱ)证明:AC⊥BD;
(Ⅲ)求二面角D-AC-O的余弦值.
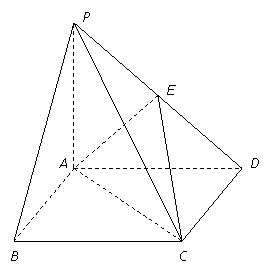
查看习题详情和答案>>(12分)如图,四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,且
,且![]() ,
,![]() 为
为![]() 中点.
中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得点
,使得点![]() 到平面
到平面![]() 的距离
的距离
为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.