题目内容
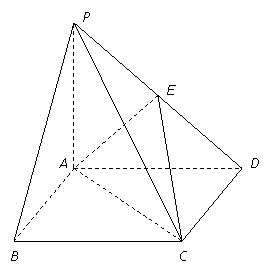
(12分)如图,四棱锥![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形,![]() ,且
,且![]() ,
,![]() 为
为![]() 中点.
中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得点
,使得点![]() 到平面
到平面![]() 的距离
的距离
为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
解析:解法一:(1)证明:∵底面![]() 为正方形,
为正方形,
∴![]() ,又
,又![]() , ∴
, ∴![]() 平面
平面![]() ,
,
∴![]() . 同理可证
. 同理可证![]() , ∴
, ∴![]() 平面
平面![]() .
.

(2)解:设![]() 为
为![]() 中点,连结
中点,连结![]() ,又
,又![]() 为
为![]() 中点,
中点,
可得![]() ,从而
,从而![]() 底面
底面![]() .
.
过 ![]() 作
作![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .
.
由三垂线定理有![]() ,
,
∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,可求得
中,可求得![]() ∴
∴![]() .
.
∴ 二面角![]() 的大小为
的大小为![]() .
.
(3)由![]() 为
为![]() 中点可知,
中点可知,
要使得点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,即要点
,即要点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
过 ![]() 作
作![]() 的垂线
的垂线![]() ,垂足为
,垂足为![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,
,
即![]() 为点
为点![]() 到平面
到平面![]() 的距离.∴
的距离.∴![]() ,∴
,∴![]() .
.
设![]() ,由
,由![]() 与
与![]() 相似可得
相似可得![]() ,∴
,∴![]() ,即
,即![]() .
.
∴在线段![]() 上存在点
上存在点![]() ,且
,且![]() 为
为![]() 中点,使得点
中点,使得点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
解法二:(Ⅰ)证明:同解www.ks5u.com法一.
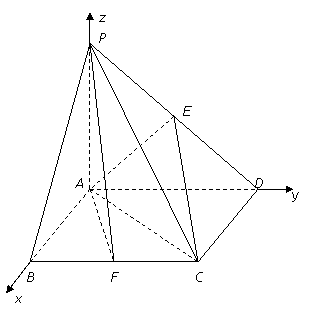
(2)解:建立如图的空间直角坐标系![]() ,
, ![]()
![]()
![]() .
.
设![]()
![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则![]()
![]() ,
,![]()
![]() .
.
又![]()
![]()
![]() 令
令![]() 则
则![]() 得
得![]()
![]() .
.
又![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,
设二面角![]() 的大小为
的大小为 ![]() ,
,
则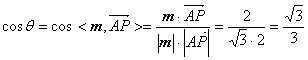 .
.
∴ 二面角![]() 的大小为
的大小为![]() .
.
(3)解:设![]()
![]()
![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则![]()
![]() ,
,![]()
![]() .又
.又![]() ,
,![]()
![]() 令
令![]() 则
则![]() 得
得![]()
![]() . 又
. 又![]()
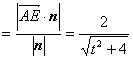 ,∴
,∴
练习册系列答案
相关题目
 中,
中, 平面
平面 ,底面
,底面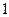 的正方形,侧棱
的正方形,侧棱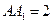 .
.
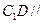 平面
平面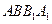 ;
;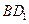 与平面
与平面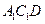 所成角的正弦值.
所成角的正弦值.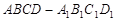 的底面是边长为
的底面是边长为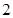 的正方形,
的正方形,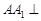 底面
底面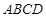 ,
, ,点
,点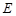 在棱
在棱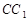 上,点
上,点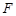 是棱
是棱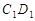 的中点
的中点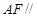 平面
平面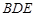 时,求
时,求 的长;
的长; 时,求二面角
时,求二面角 的余弦值。
的余弦值。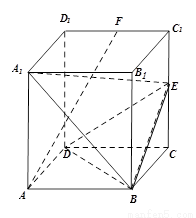
 中,
中, 平面
平面 ,底面
,底面 的正方形,侧棱
的正方形,侧棱 .
.
 平面
平面 ;
; 与平面
与平面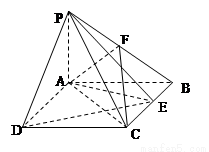
 B
B 平面ABCD,底面ABCD是边长为1的正方形,侧棱AA
平面ABCD,底面ABCD是边长为1的正方形,侧棱AA