题目内容
(本小题满分12分)
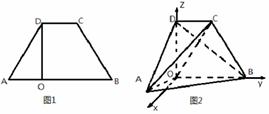
如图1，已知四边形ABCD是上、下底长分别为2和6，高DO为
的等腰梯形，将它沿DO折成
的二面角A－DO－B，如图2，连结AB，AC，BD，OC.
(Ⅰ)求三棱锥A－BOD的体积V；
(Ⅱ)证明：AC⊥BD；
(Ⅲ)求二面角D－AC－O的余弦值.
(本小题满分12分)
解：(Ⅰ)
=
. ……………4分
(Ⅱ)
，
∴
，即
. ……………………8分
(Ⅲ)由条件知
，以O为原点，OB、OD分别为
、
建立空间直角坐标系(如图)，则
，
，
，∴
，
.
设平面ACD的法向量为
，平面ACO的法向量为
，
则
，得
，
解得
，∴
.
同理得
，
∴
，由图可知，
与
的夹角和二面角D-AC-O的大小相等，
∴二面角D-AC-O的余弦值是
. ………………………12分
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
