摘要:给出以下命题: ①已知向量..满足条件++=0.且||=||=||=1.则△P1P2P3为正三角形, ②已知a>b>c,若不等式恒成立.则k∈(0,2); ③曲线y=x3在点(1,)处切线与直线x+y-3=0垂直, ④若平面α⊥平面γ,平面β∥平面γ.则α∥β. 其中正确命题的序号是 .
网址:http://m.1010jiajiao.com/timu3_id_498839[举报]
给出以下命题:①已知向量![]() ,
,![]() ,
,![]() 满足条件
满足条件![]() ,且
,且![]() ,则DP1P2P3为正三角形;②已知a>b>c,若不等式
,则DP1P2P3为正三角形;②已知a>b>c,若不等式![]() 恒成立,则kÎ(0,2);③曲线
恒成立,则kÎ(0,2);③曲线![]() 在点
在点![]() 处切线与直线x+y-3=0垂直;④若平面a^平面g,平面b∥平面g,则a∥b,其中正确命题序号是________.
处切线与直线x+y-3=0垂直;④若平面a^平面g,平面b∥平面g,则a∥b,其中正确命题序号是________.
查看习题详情和答案>>
给出以下命题:①已知向量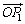 ,
,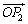 ,
,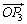 满足条件
满足条件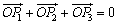 ,且
,且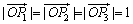 ,则DP1P2P3为正三角形;②已知a>b>c,若不等式
,则DP1P2P3为正三角形;②已知a>b>c,若不等式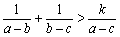 恒成立,则kÎ(0,2);③曲线
恒成立,则kÎ(0,2);③曲线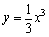 在点
在点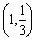 处切线与直线x+y-3=0垂直;④若平面a^平面g,平面b∥平面g,则a∥b,其中正确命题序号是________.
处切线与直线x+y-3=0垂直;④若平面a^平面g,平面b∥平面g,则a∥b,其中正确命题序号是________.
查看习题详情和答案>>
给出以下5个命题:
①曲线x2-(y-1)2=1按
=(1,-2)平移可得曲线(x+1)2-(y-3)2=1;
②设A、B为两个定点,n为常数,|
|-|
|=n,则动点P的轨迹为双曲线;
③若椭圆的左、右焦点分别为F1、F2,P是该椭圆上的任意一点,延长F1P到点M,使|F2P|=|PM|,则点M的轨迹是圆;
④A、B是平面内两定点,平面内一动点P满足向量
与
夹角为锐角θ,且满足 |
| |
| +
•
=0,则点P的轨迹是圆(除去与直线AB的交点);
⑤已知正四面体A-BCD,动点P在△ABC内,且点P到平面BCD的距离与点P到点A的距离相等,则动点P的轨迹为椭圆的一部分.
其中所有真命题的序号为 .
查看习题详情和答案>>
①曲线x2-(y-1)2=1按
| a |
②设A、B为两个定点,n为常数,|
| PA |
| PB |
③若椭圆的左、右焦点分别为F1、F2,P是该椭圆上的任意一点,延长F1P到点M,使|F2P|=|PM|,则点M的轨迹是圆;
④A、B是平面内两定点,平面内一动点P满足向量
| AB |
| AP |
| PB |
| AB |
| PA |
| AB |
⑤已知正四面体A-BCD,动点P在△ABC内,且点P到平面BCD的距离与点P到点A的距离相等,则动点P的轨迹为椭圆的一部分.
其中所有真命题的序号为
(2011•洛阳二模)给出下列命题:
①设向量
,
满足|
|=2,|
|=1,
,
的夹角为
.若向量2t
+7
与
+t
的夹角为钝角,则实数t的取值范围是(-7,-
);
②已知一组正数x1,x2,x3,x4的方差为s2=
(x12+x22+x32+x42)-4,则x1+1,x2+1,x3+1,x4+1的平均数为1
③设a,b,c分别为△ABC的角A,B,C的对边,则方程x2+2ax+b2=o与x2+2cx-b2=0有公共根的充要条件是A=90°;
④若f(n)表示n2+1(n∈N)的各位上的数字之和,如112+1=122,1+2+2=5,所以f(n)=5,记f1(n)=f(n),f2(n)=f[f1(n)],…fk+1(n)=f[fk(n)],k∈N,则f20(5)=11.
上面命题中,假命题的序号是
查看习题详情和答案>>
①设向量
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| π |
| 3 |
| e1 |
| e2 |
| e1 |
| e2 |
| 1 |
| 2 |
②已知一组正数x1,x2,x3,x4的方差为s2=
| 1 |
| 4 |
③设a,b,c分别为△ABC的角A,B,C的对边,则方程x2+2ax+b2=o与x2+2cx-b2=0有公共根的充要条件是A=90°;
④若f(n)表示n2+1(n∈N)的各位上的数字之和,如112+1=122,1+2+2=5,所以f(n)=5,记f1(n)=f(n),f2(n)=f[f1(n)],…fk+1(n)=f[fk(n)],k∈N,则f20(5)=11.
上面命题中,假命题的序号是
②
②
(写出所有假命题的序号).(本题满分20分,其中第1小题4分,第2小题6分,第3小题10分.)
平面直角坐标系![]() 中,已知
中,已知![]() ,…,
,…,![]() 是直线
是直线![]() 上的
上的![]() 个点(
个点(![]() ,
,![]() 、
、![]() 均为非零常数).
均为非零常数).
(1)若数列![]() 成等差数列,求证:数列
成等差数列,求证:数列![]() 也成等差数列;
也成等差数列;
(2)若点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() ,求
,求![]() 的值;
的值;
(3)若点![]() 满足
满足![]() ,我们称
,我们称![]() 是向量
是向量![]() ,
,![]() ,…,
,…,![]() 的线性组合,
的线性组合,![]() 是该线性组合的系数数列.
是该线性组合的系数数列.
当![]() 是向量
是向量![]() ,
,![]() ,…,
,…,![]() 的线性组合时,请参考以下线索:
的线性组合时,请参考以下线索:
① 系数数列![]() 需满足怎样的条件,点
需满足怎样的条件,点![]() 会落在直线
会落在直线![]() 上?
上?
② 若点![]() 落在直线
落在直线![]() 上,系数数列
上,系数数列![]() 会满足怎样的结论?
会满足怎样的结论?
③ 能否根据你给出的系数数列![]() 满足的条件,确定在直线
满足的条件,确定在直线![]() 上的点
上的点![]() 的个数或坐标?
的个数或坐标?
试提出一个相关命题(或猜想)并开展研究,写出你的研究过程.【本小题将根据你提出的命题(或猜想)的完备程度和研究过程中体现的思维层次,给予不同的评分】
查看习题详情和答案>>