摘要：23．(2005年高考·全国卷II·理20文20)) 如图.四棱锥P-ABCD中.底面ABCD为矩形.PD⊥底面ABCD.AD=PD.E.F分别为CD.PB的中点. (Ⅰ)求证:EF⊥平面PAB, (Ⅱ)设AB=BC.求AC与平面AEF所成的角的大小. 本小题主要考查直线与平面垂直.直线与平面所成角的有关知识.及思维能力和空间想象能力.满分12分. 证明:(Ⅰ)证明:连结EP. 底面ABCD.DE在平面ABCD内.. 又CE＝ED.PD＝AD＝BC. F为PB中点.∴由三垂线定理得.∴在中.PF＝AF. 又PE＝BE＝EA. PB.FA为平面PAB内的相交直线.∴EF平面PAB. (Ⅱ)解:不妨设BC＝1.则AD＝PD＝1.AB＝.PA＝.AC＝ ∴PAB为等腰直角三角形.且PB＝2.F为其斜边中点.BF＝1.且AFPB. PB与平面AEF内两条相交直线EF.AF都垂直.∴PB平面AEF. 连结BE交AC于G.作GH∥BP交EF于H.则GH平面AEF.GAH为AC与平面AEF所成的角. 由EGC∽BGA可知EG＝. 由ECH∽EBF可知. ∴ ∴与平面所成的角为
网址：http://m.1010jiajiao.com/timu3_id_498753[举报]
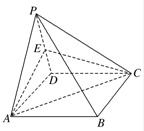如图，四棱锥P-ABCD的底面是矩形，侧面PAD是正三角形，且侧面PAD⊥底面ABCD，E为侧棱PD的中点．（1）求证：PB∥平面EAC；
（2）若AD=AB，试求二面角A-PC-D的正切值． 查看习题详情和答案>>
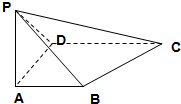如图，四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为直角梯形，AB∥CD，BA⊥AD，且CD=2AB．若AB=AD=a，直线PB与CD所成角为450，（1）求四棱锥P-ABCD的体积VP-ABCD；
（2）求二面角P-CD-B的大小．
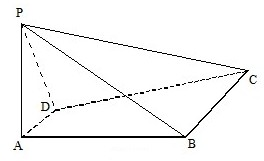如图，四棱锥P-ABCD中，PA⊥平面ABCD，四边形ABCD是直角梯形，其中DA⊥AB，AD∥BC．PA=2AD=BC=2AB=2| 2 |
（1）求异面直线PC与AD所成角的大小；
（2）若平面ABCD内有一经过点C的曲线E，该曲线上的任一动点Q都满足PQ与AD所成角的大小恰等PC与AD所成角．试判断曲线E的形状并说明理由；
（3）在平面ABCD内，设点Q是（2）题中的曲线E在直角梯形ABCD内部（包括边界）的一段曲线CG上的动点，其中G为曲线E和DC的交点．以B为圆心，BQ为半径的圆分别与梯形的边AB、BC交于M、N两点．当Q点在曲线段GC上运动时，试提出一个研究有关四面P-BMN的问题（如体积、线面、面面关系等）并尝试解决．
（说明：本小题将根据你提出的问题的质量和解决难度分层评分；本小题的计算结果可以使用近似值，保留3位小数） 查看习题详情和答案>>
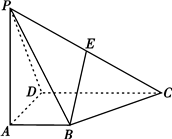如图，四棱锥P-ABCD的底面ABCD为一直角梯形，其中BA⊥AD，CD⊥AD，CD=AD=2AB，PA⊥底面ABCD，E是PC的中点．
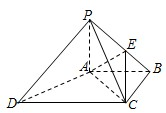如图，四棱锥P-ABCD中，PA⊥底面ABCD，PC⊥AD．底面ABCD为梯形，AB∥DC，AB⊥BC．PA=AB=BC，点E在棱PB上，且PE=2EB．