摘要：如果在区间[1, 3]上.函数f (x)=x2+px+q与g(x)=x+在同一点取得相同的最小值.那么下列说法不对的是( ). (A)f (x)≥3 (x∈[1, 2]) (B)f (x)≤4 (x∈[1, 2]) (C)f (x)在x∈[1, 2]上单调递增 (D)f (x)在x∈[1, 2]上是减函数
网址：http://m.1010jiajiao.com/timu3_id_498681[举报]
（13分）设函数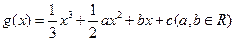
的图象经过原点，在其图象上一点P（x，y）处的切线的斜率记为
.
（1）若方程=0有两个实根分别为-2和4,求的表达式；
（2）若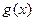
在区间[-1,3]上是单调递减函数,求
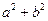的最小值.
已知函数f(x)＝alnx－ax－3(a∈R)．
(1)求函数f(x)的单调区间；
(2)函数y＝f(x)的图像在x＝4处的切线的斜率为
，若函数g(x)＝
x3＋x2[f′(x)＋
]在区间(1,3)上不是单调函数，求m的取值范围．
m(x－1)2－2x＋3＋ln x，m≥1.
时，求函数f(x)在区间[1,3]上的极小值；
在区间[1,3]上的极值。
在区间[1,3]上的极值。