摘要: 设函数f(x)=x+的图象为c1,c1关于点A(2.1)对称的图象为c2,c2对应的函数为g(x). (1)求g(x)的解析表达式, (2)解不等式logag(x)<loga (a>0.且a≠1)
网址:http://m.1010jiajiao.com/timu3_id_498459[举报]
(本小题满分12分)
设![]() =(2cosx,1),
=(2cosx,1),![]() =(cosx,
=(cosx,![]() sin2x),f(x)=
sin2x),f(x)=![]() ·
·![]() ,x
,x![]() R.
R.
⑴ 若f(x)=0且x![]() [-,],求x的值.
[-,],求x的值.
⑵ 若函数g(x)=cos(wx-)+k(w>0, k![]() R)与f(x)的最小正周期相同,且g(x)的图象过点(,2),求函数g(x)的值域及单调递增区间.
R)与f(x)的最小正周期相同,且g(x)的图象过点(,2),求函数g(x)的值域及单调递增区间.
本小题满分12分)
已知函数f(x)=lnx-ax2+(2-a)x.
(I)讨论f(x)的单调性;
(II)设a>0,证明:当0<x<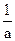 时,f(
时,f(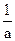 +x)>f(
+x)>f(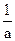 -x);
-x);
(III)若函数y=f(x)的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:f’( x0)<0.
 .
. 的图象在点
的图象在点 处的切线为直线l,且直线l与圆
处的切线为直线l,且直线l与圆 相切,求a的值;
相切,求a的值; 时,求函数f(x)的单调区间.
时,求函数f(x)的单调区间.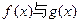 图象交于不同的两点;
图象交于不同的两点;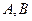 ,求线段AB在x轴上的射影A1B1的长的取值范围。
,求线段AB在x轴上的射影A1B1的长的取值范围。