摘要：13．已知抛物线C:y2＝2px(p>0)过点A． (1)求抛物线C的方程.并求其准线方程, (2)是否存在平行于OA(O为坐标原点)的直线l.使得直线l与抛物线C有公共点.且直线OA与l的距离等于?若存在.求直线l的方程,若不存在.说明理由． 解:代入y2＝2px.得(-2)2＝2p·1.所以p＝2. 故所求抛物线C的方程为y2＝4x.其准线方程为x＝-1. (2)假设存在符合题意的直线l.其方程为y＝-2x+t. 由得y2+2y-2t＝0. 因为直线l与抛物线C有公共点.所以Δ＝4+8t≥0.解得t≥-. 由直线OA与l的距离d＝可得＝.解得t＝±1. 因为-1∉.1∈. 所以符合题意的直线l存在.其方程为2x+y-1＝0.
网址：http://m.1010jiajiao.com/timu3_id_497675[举报]
已知抛物线C：y2＝2px(p＞0)，直线l交C于E、F两点．
(1)求证：命题“若直线l过点A(2p，0)，则∠EOF＝90°(O为坐标原点)”是真命题；
(2)写出(1)中命题的逆命题，判断它是真命题还是假命题，并说明理由；
(3)将点A(2p，0)向右或向左移动为点A(c，0)，直线l过点A交C于E、F两点．当c＞2p及0＜c＜2p时，分别猜测∠EOF大小的变化情况(只须写出结论，不必证明)．
已知抛物线C：y2＝2px(p>0)，M点的坐标为(12,8)，N点在抛物线C上，且满足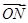
＝
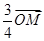，O为坐标原点．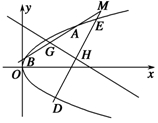
(1)求抛物线C的方程；
(2)以M点为起点的任意两条射线l1，l2的斜率乘积为1，并且l1与抛物线C交于A，B两点，l2与抛物线C交于D，E两点，线段AB，DE的中点分别为G，H两点．求证：直线GH过定点，并求出定点坐标．
已知抛物线C：y2＝2px(p>0)的焦点为F，抛物线C与直线l1：y＝－x的一个交点的横坐标为8.
(1)求抛物线C的方程；
(2)不过原点的直线l2与l1垂直，且与抛物线交于不同的两点A，B，若线段AB的中点为P，且|OP|＝|PB|，求△FAB的面积．
| |||||
．
与C相交于M，N两点，且A，M，B，N四点在同一个圆上，求直线l的方程．
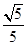？若存在，求出直线l的方程；若不存在，说明理由．