摘要：10．设x1.x2∈R.常数a＞0.定义运算“* :x1]x*a))的轨迹方程是 ． 解析:由y＝.得y2＝x*a＝(x+a)2-(x-a)2＝4ax(y≥0)． 答案:y2＝4ax(y≥0)
网址：http://m.1010jiajiao.com/timu3_id_497672[举报]
设x1、x2∈R，常数a＞0，定义运算“*”：x1*x2=（ x1+x2）2-（ x1-x2）2，若x≥0，则动点P（x，
）的轨迹是（ ）
| x*a |
| A、圆 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
设x1、x2∈R，常数a＞0，定义运算“⊕”：x1⊕x2=（x1+x2）2，定义运算“?”：x1?x2=（x1-x2）2；对于两点A（x1，y1）、B（x2，y2），定义d(AB)=
．
（1）若x≥0，求动点P（x，
） 的轨迹C；
（2）已知直线l1 ： y=
x+1与（1）中轨迹C交于A（x1，y1）、B（x2，y2）两点，若
=8
，试求a的值；
（3）在（2）中条件下，若直线l2不过原点且与y轴交于点S，与x轴交于点T，并且与（1）中轨迹C交于不同的两点P、Q，试求
+
的取值范围．
查看习题详情和答案>>
| y1?y2 |
（1）若x≥0，求动点P（x，
| (x⊕a)-(x?a) |
（2）已知直线l1 ： y=
| 1 |
| 2 |
| (x1?x2)+(y1?y2) |
| 15 |
（3）在（2）中条件下，若直线l2不过原点且与y轴交于点S，与x轴交于点T，并且与（1）中轨迹C交于不同的两点P、Q，试求
| |d(ST)| |
| |d(SP)| |
| |d(ST)| |
| |d(SQ)| |
设x1、x2∈R，常数a＞0，定义运算“*”：x1*x2=（ x1+x2）2-（ x1-x2）2，若x≥0，则动点P（x，
）的轨迹是（ ）
查看习题详情和答案>>
| x*a |
| A．圆 | B．椭圆的一部分 |
| C．双曲线的一部分 | D．抛物线的一部分 |
)的轨迹是( )
(B)椭圆的一部分
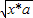）的轨迹是（ ）