题目内容
设x1、x2∈R,常数a>0,定义运算“⊕”:x1⊕x2=(x1+x2)2,定义运算“?”:x1?x2=(x1-x2)2;对于两点A(x1,y1)、B(x2,y2),定义d(AB)=| y1?y2 |
(1)若x≥0,求动点P(x,
| (x⊕a)-(x?a) |
(2)已知直线l1 : y=
| 1 |
| 2 |
| (x1?x2)+(y1?y2) |
| 15 |
(3)在(2)中条件下,若直线l2不过原点且与y轴交于点S,与x轴交于点T,并且与(1)中轨迹C交于不同的两点P、Q,试求
| |d(ST)| |
| |d(SP)| |
| |d(ST)| |
| |d(SQ)| |
分析:(1)设y=
,根据新定义运算得出:y2=(x⊕a)-(x?a)=(x+a)2-(x-a)2=4ax,从而得出的轨迹方程即可;
(2)先将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用根据新定义运算即可求得a值,从而解决问题;
(3)根据新定义运算得到:d(AB)=
=|y1-y2|,从而
+
=
+
设直线l2:x=my+c,分别过P、Q作PP1⊥y轴,QQ1⊥y轴,垂足分别为P1、Q1,有
+
=
+
=
+
.由
先将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用基本不等式即可求得试求
+
的取值范围.
| (x⊕a)-(x?a) |
(2)先将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系利用根据新定义运算即可求得a值,从而解决问题;
(3)根据新定义运算得到:d(AB)=
| y1?y2 |
| |d(ST)| |
| |d(SP)| |
| |d(ST)| |
| |d(SQ)| |
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
设直线l2:x=my+c,分别过P、Q作PP1⊥y轴,QQ1⊥y轴,垂足分别为P1、Q1,有
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
| |OT| |
| |PP1| |
| |OT| |
| |QQ1| |
| |c| |
| |xP| |
| |c| |
| |xQ| |
|
| |d(ST)| |
| |d(SP)| |
| |d(ST)| |
| |d(SQ)| |
解答: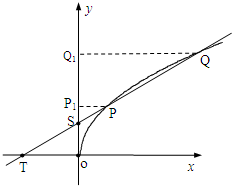 解:(1)设y=
解:(1)设y=
,
则y2=(x⊕a)-(x?a)=(x+a)2-(x-a)2=4ax,
又由y=
≥0,
可得P(x,
) 的轨迹方程为y2=4ax(y≥0),轨迹C为顶点在原点,焦点为(a,0)的抛物线在x轴上及第一象限的内的部分;
(2)由已知可得
,整理得x2+(4-16a)x+4=0,
由△=(4-16a)2-16=162a2-8×16a≥0,得a≥
或a≤0.
∵a>0,∴a≥
.
∴
=
=
=
=
=8
,
解得a=2或a=-
(舍).
(3)∵d(AB)=
=|y1-y2|,
∴
+
=
+
设直线l2:x=my+c,
依题意m≠0,c≠0,则T(c,0)
分别过P、Q作PP1⊥y轴,QQ1⊥y轴,垂足分别为P1、Q1,
则
+
=
+
=
+
.
由
消去y得x2-(2c+8m2)x+c2=0.
∴
+
=|c|(
+
)≥2|c|
=2|c|
=2.
∵xP、xQ取不相等的正数,∴取等的条件不成立,
∴
+
的取值范围是(2,+∞).
 解:(1)设y=
解:(1)设y=| (x⊕a)-(x?a) |
则y2=(x⊕a)-(x?a)=(x+a)2-(x-a)2=4ax,
又由y=
| (x⊕a)-(x?a) |
可得P(x,
| (x⊕a)-(x?a) |
(2)由已知可得
|
由△=(4-16a)2-16=162a2-8×16a≥0,得a≥
| 1 |
| 2 |
∵a>0,∴a≥
| 1 |
| 2 |
∴
| (x1?x2)+(y1?y2) |
| (x1-x2)2+(y1-y2)2 |
(x1-x2)2+(
|
| ||
| 2 |
| (x1+x2)2-4x1x2 |
| ||
| 2 |
| (4-16a)2-16 |
| 15 |
解得a=2或a=-
| 1 |
| 2 |
(3)∵d(AB)=
| y1?y2 |
∴
| |d(ST)| |
| |d(SP)| |
| |d(ST)| |
| |d(SQ)| |
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
设直线l2:x=my+c,
依题意m≠0,c≠0,则T(c,0)
分别过P、Q作PP1⊥y轴,QQ1⊥y轴,垂足分别为P1、Q1,
则
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
| |OT| |
| |PP1| |
| |OT| |
| |QQ1| |
| |c| |
| |xP| |
| |c| |
| |xQ| |
由
|
∴
| |ST| |
| |SP| |
| |ST| |
| |SQ| |
| 1 |
| |xP| |
| 1 |
| |xQ| |
|
|
∵xP、xQ取不相等的正数,∴取等的条件不成立,
∴
| |d(ST)| |
| |d(SP)| |
| |d(ST)| |
| |d(SQ)| |
点评:本题抽象函数、新定义函数类型的概念,不等式的性质,放缩法的技巧,对于新定义类型问题,在解答时要先充分理解定义才能答题,避免盲目下笔,遇到困难才来重头读题,费时费力,另外要在充分抓住定义的基础上,对式子的处理要灵活,各个式子的内在联系要充分挖掘出来,可现有结论向上追溯,看看需要哪些条件才能得出结果,再来寻求转化取得这些条件.属中档题.

练习册系列答案
相关题目
设x1、x2∈R,常数a>0,定义运算“*”:x1*x2=( x1+x2)2-( x1-x2)2,若x≥0,则动点P(x,
)的轨迹是( )
| x*a |
| A、圆 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |