摘要:在右图所示的几何体中,平面PAC⊥平面ABC,PM∥BC,PA=PC,AC=1,BC=2PM=2,AB=若该几何体的侧视图的面积为 (1)求证:PA⊥BC; (2)画出该几何体的正视图,并求其面积S; (3)求出多面体A-BMPC的体积V. 解:(1)证明:AC=1,BC=2,AB=, ∴AC2+BC2=AB2. ∴AC⊥BC.又∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC, ∴BC⊥平面PAC.又∵PA⊂平面PAC,∴PA⊥BC. (2)设几何体的正视图如图所示: ∵PA=PC,取AC的中点D,连接PD,则PD⊥AC. 又平面PAC⊥平面ABC, ∴PD⊥平面ABC. ∴几何体侧视图的面积=AC·PD =×1×PD=. ∴PD=.易知△PAC是边长为1的正三角形. ∴正视图的面积是上、下底边长分别为1和2,PD的长为高的直角梯形的面积. ∴S= (3)取PC的中点N,连接AN,由△PAC是边长为1的正三角形,可知AN⊥PC,由(1)知BC⊥平面PAC, ∴AN⊥BC,∴AN⊥平面PCBM. ∴AN是四棱锥A-PCBM的高,且AN= 由BC⊥平面PAC,可知BC⊥PC. 由PM∥BC,可知四边形PCBM是上、下底边长分别为1和2,PC的长1为高的直角梯形. 其面积S′=,∴V=S′·AN=
网址:http://m.1010jiajiao.com/timu3_id_497662[举报]
在如右图所示的几何体中,四边形A![]() BCD是正方形,MA⊥平面ABCD,PD∥MA,E、G、F分别为MB、PB、PC的中点,且AD=PD=2MA.
BCD是正方形,MA⊥平面ABCD,PD∥MA,E、G、F分别为MB、PB、PC的中点,且AD=PD=2MA.
(1)求证:平面EFG⊥平面PDC;
(2)求三棱锥P-MAB与四棱锥P-ABCD的体积之比.

查看习题详情和答案>>
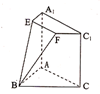 (2012•宝鸡模拟)在如图所示的几何体中,四边形ACC1A1是矩形,FC1∥BC,EF∥A1C1,∠BCC1=90°,点A、B、E、A1在一个平面内,AB=BC=CC1=2,AC=2
(2012•宝鸡模拟)在如图所示的几何体中,四边形ACC1A1是矩形,FC1∥BC,EF∥A1C1,∠BCC1=90°,点A、B、E、A1在一个平面内,AB=BC=CC1=2,AC=2| 2 |
(1)证明:A1E∥AB;
(2)证明:平面CC1FB⊥平面AA1EB.
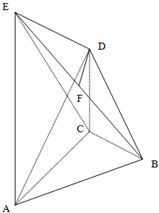 在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,
在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
(Ⅰ)求证:DF∥平面ABC;
(Ⅱ)求证:DF⊥平面ABE;
(Ⅲ)求三棱锥D-BCE的体积. 查看习题详情和答案>>
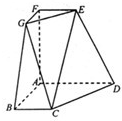 在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.
在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC. 在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD为平行四边形,∠ACB=90°,EF∥BC,AC=BC=
在如图所示的几何体中,平面ACE⊥平面ABCD,四边形ABCD为平行四边形,∠ACB=90°,EF∥BC,AC=BC=