题目内容
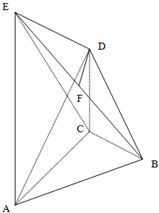 在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,
在如图所示的几何体中,AE⊥平面ABC,CD∥AE,F是BE的中点,AC=BC=1,∠ACB=90°,AE=2CD=2.
(Ⅰ)求证:DF∥平面ABC;
(Ⅱ)求证:DF⊥平面ABE;
(Ⅲ)求三棱锥D-BCE的体积.
分析:(Ⅰ)取AB的中点M,证明FM平行且等于CD,四边形FMCD为平行四边形,可得DF∥CM,从而证明DF∥平面ABC.
(II)由等腰三角形的性质可得CM⊥AB,再由CM⊥AE,可得CM⊥面ABE,DF⊥平面ABE.
(III)利用 V三棱锥D-BCE =V 三棱锥E-BCD =V三棱锥A-BCD=
S△BCD×AC,求得结果.
(II)由等腰三角形的性质可得CM⊥AB,再由CM⊥AE,可得CM⊥面ABE,DF⊥平面ABE.
(III)利用 V三棱锥D-BCE =V 三棱锥E-BCD =V三棱锥A-BCD=
| 1 |
| 3 |
解答: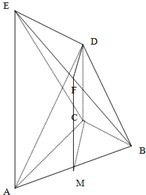 解:(Ⅰ)证明:取AB的中点M,连接FM,CM,
解:(Ⅰ)证明:取AB的中点M,连接FM,CM,
在△ABE中,F,M分别EB,AB的中点,∴FM∥
AE,且FM=
AE.
又∵CD∥AE,CD=
AE,∴FM平行且等于CD,
∴四边形FMCD为平行四边形,∴DF∥CM,又∵CM⊆平面ABC,DF?平面ABC,
∴DF∥平面ABC.
(II)证明:∵AC=BC,M为AB的中点,∴CM⊥AB,又AE⊥平面ABC,
CM⊆平面ABC,∴CM⊥AE. 又AE∩AB=A,∴CM⊥面ABE,由(1)得DF∥CM,
∴DF⊥平面ABE.
(III)解:∵CD∥AE,∴V三棱锥D-BCE =V 三棱锥E-BCD =V三棱锥A-BCD,
∴V三棱锥D-BCE=
S△BCD•AC=
×
×1×1×1=
.
 解:(Ⅰ)证明:取AB的中点M,连接FM,CM,
解:(Ⅰ)证明:取AB的中点M,连接FM,CM,在△ABE中,F,M分别EB,AB的中点,∴FM∥
| 1 |
| 2 |
| 1 |
| 2 |
又∵CD∥AE,CD=
| 1 |
| 2 |
∴四边形FMCD为平行四边形,∴DF∥CM,又∵CM⊆平面ABC,DF?平面ABC,
∴DF∥平面ABC.
(II)证明:∵AC=BC,M为AB的中点,∴CM⊥AB,又AE⊥平面ABC,
CM⊆平面ABC,∴CM⊥AE. 又AE∩AB=A,∴CM⊥面ABE,由(1)得DF∥CM,
∴DF⊥平面ABE.
(III)解:∵CD∥AE,∴V三棱锥D-BCE =V 三棱锥E-BCD =V三棱锥A-BCD,
∴V三棱锥D-BCE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题考查证明线面平行、线面垂直的方法,求棱锥的体积,体现了数形结合的数学思想,证明CM⊥面ABE,是解题的
关键.
关键.

练习册系列答案
相关题目
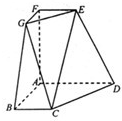 在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.
在如图所示的几何体中,四边形ABCD、ADEF、ABGF均为全等的直角梯形,且BC∥AD,AB=AD=2BC.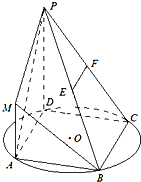 在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP=
在如图所示的几何体中,平行四边形ABCD的顶点都在以AC为直径的圆O上,AD=CD=DP=a,AP=CP= (2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1,
(2012•朝阳区一模)在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥平面ABCD,EF∥AB,AB=2,EF=1, 在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.
在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AB=2BC,∠ABC=60°,AC⊥FB.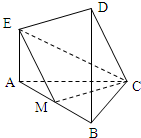 在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中,EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,AC=BC=BD=2AE=2,M是AB的中点.