摘要:如图.梯形ABCD中.AD∥BC.AB=CD.AD=2.BC=6.∠B=60°.则梯形ABCD的周长是( ) A.12 B.14 C.16 D.18 考点:等腰梯形的性质,含30度角的直角三角形. 分析:从上底的两个端点向下底作垂线.构造直角三角形和矩形.求得直角三角形的直角边的长利用告诉的锐角的度数求得等腰梯形的腰长.然后求得等腰梯形的周长. 解答:解:作AE⊥BC于E点.DF⊥BC于F点. ∵AD∥BC. ∴四边形AEFD为矩形. ∵AD=2.BC=6. ∴EF=AD=2.BE=CF=÷2=2. ∵∠B=60°. ∴AB=DC=2BE=2×2=4. ∴等腰梯形的周长为:AB+BC+CD+DA=4+6+4+2=16. 故选C. 点评:本题考查了等腰梯形的性质及含30°的直角三角形的性质.解题的关键是正确的作辅助线构造直角三角形和矩形.从而求得等腰梯形的高.
网址:http://m.1010jiajiao.com/timu3_id_496972[举报]
如图,梯形ABCD中,AB∥CD,AC平分∠BAD,且AC⊥BC,BC=3厘米,AC=6厘米,则△ACD的面积是( )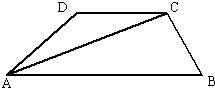

A、
| ||
| B、9平方厘米 | ||
| C、6平方厘米 | ||
| D、3平方厘米 |
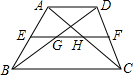 如图,梯形ABCD中,AD∥BC,EF是中位线,对角线BD、AC分别与EF相交于G、H,若GH:BC=1:3,则AD:BC的值是
如图,梯形ABCD中,AD∥BC,EF是中位线,对角线BD、AC分别与EF相交于G、H,若GH:BC=1:3,则AD:BC的值是 线段BE上取一点G,使得BF=BG,连接CG.
线段BE上取一点G,使得BF=BG,连接CG.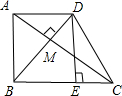 如图,梯形ABCD中,AD∥BC,对角线AC⊥BD,垂足为点M,过点D作DE⊥BC于点E,AC=8,BD=6,则梯形ABCD的高DE=
如图,梯形ABCD中,AD∥BC,对角线AC⊥BD,垂足为点M,过点D作DE⊥BC于点E,AC=8,BD=6,则梯形ABCD的高DE=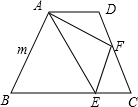 如图,梯形ABCD中,F是CD的中点,AF⊥AB,E是BC边上的一点,且AE=BE.若AB=m(m为常数),则EF的长为
如图,梯形ABCD中,F是CD的中点,AF⊥AB,E是BC边上的一点,且AE=BE.若AB=m(m为常数),则EF的长为