摘要： 如图(1).△ABC与△EFD为等腰直角三角形.AC与DE重合.AB=EF=9.∠BAC＝∠DEF＝90°.固定△ABC.将△EFD绕点A 顺时针旋转.当DF边与AB边重合时.旋转中止.不考虑旋转开始和结束时重合的情况.设DE.DF分别交BC于G.H点.如图(2). (1)问:始终与△AGC相似的三角形有 及 , (2)设CG＝x.BH＝y.求y关于x的函数关系式(只要求根据2的情况说明理由), (3)问:当x为何值时.△AGH是等腰三角形? [解](1)△HGA及△HAB, 可知△AGC∽△HAB ∴.即. 所以. (3)当CG＜时.∠GAC=∠H＜∠HAC.∴AC＜CH ∵AG＜AC.∴AG＜GH 又AH＞AG.AH＞GH 此时.△AGH不可能是等腰三角形, 当CG=时.G为BC的中点.H与C重合.△AGH是等腰三角形, 此时.GC=.即x= 当CG＞时.由(1)可知△AGC∽△HGA 所以.若△AGH必是等腰三角形.只可能存在AG=AH 若AG=AH.则AC=CG.此时x=9 综上.当x=9或时.△AGH是等腰三角形．
网址：http://m.1010jiajiao.com/timu3_id_496617[举报]
12、如图，△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于D．给出下列结论：①∠AFC=∠C；
②DE=CF；
③△ADE∽△FDB；
④∠BFD=∠CAF
其中正确的结论是
①③④
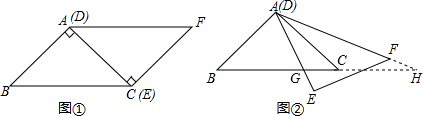
．如图①，△ABC与△EFD为等腰直角三角形，AC与DE重合，AB=AC=EF=9，∠BAC=∠DEF=90°．如图②所示，现固定△ABC，将△EFD绕点A顺时针旋转，当AE边与AB边重合时，旋转中止，若不考虑旋转开始和结束时这两种特殊的情形，设DE、DF（或它们的延长线）分别交BC（或它的延长线）于G、H两点，设CG=x．
（1）始终与△AGC相似的三角形有
（2）设BH=y，求y关于x的函数关系式；
（3）当x为何值时，△AGH是等腰三角形？
查看习题详情和答案>>
（1）始终与△AGC相似的三角形有
△HAB
△HAB
及△HGA
△HGA
；（2）设BH=y，求y关于x的函数关系式；
（3）当x为何值时，△AGH是等腰三角形？
（2011•海曙区模拟）如图，△ABC与△EDF中，点A、D、B、E在一直线上，∠A=∠E，AC=EF，在下列条件中随机抽取一个作为补充条件：①∠C=∠F，②AD=BE，③BC=DF，④BC∥DF，能使△ABC≌△EDF的概率是（ ）
如图，△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，点F在BC上，且AB交EF于D．
29、如图，△ABC与△A′B′C′关于直线MN对称，△A′B′C′与△A″B″C″关于直线EF对称．