题目内容
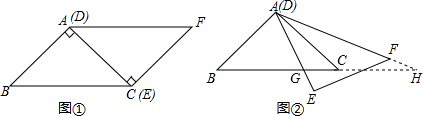
如图①,△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF=90°.如图②所示,现固定△ABC,将△EFD绕点A顺时针旋转,当AE边与AB边重合时,旋转中止,若不考虑旋转开始和结束时这两种特殊的情形,设DE、DF(或它们的延长线)分别交BC(或它的延长线)于G、H两点,设CG=x.
(1)始终与△AGC相似的三角形有
(2)设BH=y,求y关于x的函数关系式;
(3)当x为何值时,△AGH是等腰三角形?
(1)始终与△AGC相似的三角形有
△HAB
△HAB
及△HGA
△HGA
;(2)设BH=y,求y关于x的函数关系式;
(3)当x为何值时,△AGH是等腰三角形?

分析:(1)根据△ABC与△EFD为等腰直角三角形,AC与DE重合,利用相似三角形的判定定理即可得出结论.
(2)由△AGC∽△HAB,利用其对应边成比例列出关于x、y的关系式:9:y=x:9即可.
(3)此题要采用分类讨论的思想,当CG<
BC时,当CG=
BC时,当CG>
BC时分别得出即可.
(2)由△AGC∽△HAB,利用其对应边成比例列出关于x、y的关系式:9:y=x:9即可.
(3)此题要采用分类讨论的思想,当CG<
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解: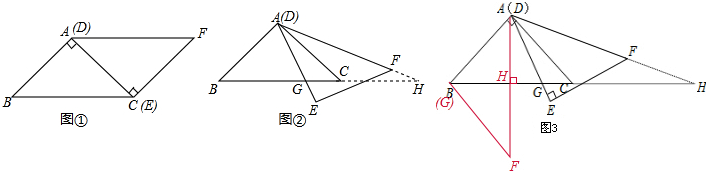
(1)∵△ABC与△EFD为等腰直角三角形,AC与DE重合,
∵∠H+∠HAC=45°,∠HAC+∠CAG=45°,
∴∠H=∠CAG,
∵∠ACG=∠B=45°,
∴△AGC∽△HAB,
∴同理可得出:△AGC∽△HGA,
∴始终与△AGC相似的三角形有△HAB和△HGA;
故答案为:△HAB和△HGA.
(2)∵△AGC∽△HAB,
∴AC:HB=GC:AB,即9:y=x:9,
∴y=
,
∵AB=AC=9,∠BAC=90°,
∴BC=
=
=9
.
答:y关于x的函数关系式为y=
(0<x<9
);
(3)①当CG<
BC时,∠GAC=∠H<∠HAC,
∴AC<CH,
∵AG<AC,
∴AG<CH<GH,
又∵AH>AG,AH>GH,
此时,△AGH不可能是等腰三角形,
②当CG=
BC时,G为BC的中点,H与C重合,△AGH是等腰三角形,
此时,GC=
,即x=
,
③当CG>
BC时,由(1)△AGC∽△HGA,
∴,若△AGH必是等腰三角形,只可能存在GH=AH,若GH=AH,则AC=CG,此时x=9,
如图3,当CG=BC时,
注意:DF才旋转到与BC垂直的位置,
此时B,E,G重合,∠AGH=∠GAH=45°,
∴△AGH为等腰三角形,所以CG=9
.
综上所述,当x=9或x=
或9
时,△AGH是等腰三角形.

(1)∵△ABC与△EFD为等腰直角三角形,AC与DE重合,
∵∠H+∠HAC=45°,∠HAC+∠CAG=45°,
∴∠H=∠CAG,
∵∠ACG=∠B=45°,
∴△AGC∽△HAB,
∴同理可得出:△AGC∽△HGA,
∴始终与△AGC相似的三角形有△HAB和△HGA;
故答案为:△HAB和△HGA.
(2)∵△AGC∽△HAB,
∴AC:HB=GC:AB,即9:y=x:9,
∴y=
| 81 |
| x |
∵AB=AC=9,∠BAC=90°,
∴BC=
| AB2+AC2 |
| 92+92 |
| 2 |
答:y关于x的函数关系式为y=
| 81 |
| x |
| 2 |
(3)①当CG<
| 1 |
| 2 |
∴AC<CH,
∵AG<AC,
∴AG<CH<GH,
又∵AH>AG,AH>GH,
此时,△AGH不可能是等腰三角形,
②当CG=
| 1 |
| 2 |
此时,GC=
9
| ||
| 2 |
9
| ||
| 2 |
③当CG>
| 1 |
| 2 |
∴,若△AGH必是等腰三角形,只可能存在GH=AH,若GH=AH,则AC=CG,此时x=9,
如图3,当CG=BC时,
注意:DF才旋转到与BC垂直的位置,
此时B,E,G重合,∠AGH=∠GAH=45°,
∴△AGH为等腰三角形,所以CG=9
| 2 |
综上所述,当x=9或x=
9
| ||
| 2 |
| 2 |
点评:此题主要考查学生对相似三角形的判定与性质,等腰三角形的性质,等腰直角三角形的性质,旋转的性质等知识点的理解和掌握,综合性较强,难易程度适中,是一道很典型的题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 10、如图,在△ABC与△ADE中,∠BAD=∠CAE,BC=DE,且点C在DE上,若添加一个条件,能判定△ABC≌△ADE,这个条件是( )
10、如图,在△ABC与△ADE中,∠BAD=∠CAE,BC=DE,且点C在DE上,若添加一个条件,能判定△ABC≌△ADE,这个条件是( ) 26、如图,在△ABC与△DEF中BF=CE,AB=DE,AC=DF.求证:OF=OC.
26、如图,在△ABC与△DEF中BF=CE,AB=DE,AC=DF.求证:OF=OC. 7、如图,三角形ABC与下列相似但不全等的是( )
7、如图,三角形ABC与下列相似但不全等的是( ) 如图,Rt△ABC与Rt△A′B′C′关于直线l对称,则线段AC的长为( )
如图,Rt△ABC与Rt△A′B′C′关于直线l对称,则线段AC的长为( ) 如图,在△ABC与△ADC中,点E在边AC上,∠1=∠2,∠3=∠4.说明:DC=BC.
如图,在△ABC与△ADC中,点E在边AC上,∠1=∠2,∠3=∠4.说明:DC=BC.