摘要： 如图.已知等腰Rt△ABC的直角边长为1.以Rt△ABC的斜边AC为直角边.画第二个等腰Rt△ACD.再以Rt△ACD的斜边AD为直角边.画第三个等腰Rt△ADE.-.依此类推直到第五个等腰Rt△AFG.则由这五个等腰直角三角形所构成的图形的面积为 ． [答案]
网址：http://m.1010jiajiao.com/timu3_id_496615[举报]
如图，已知等腰Rt△ABC直角边长为1，以它的斜边AC为直角边画第二个等腰Rt△ACD，再以斜边AD为直角边画第三个Rt△ADE…，依此类推，AC长为| 2 |
2
| 2 |
2
，第4个等腰三角形斜边AF长=| 2 |
4
4
，则第n个等腰直角三角形斜边长=（
）n
| 2 |
（
）n
．| 2 |
如图，已知等腰Rt△ABC中，∠ACB=90°，AC=BC=4，D为△ABC的一个外角∠ABF的平分线上一点，且∠ADC=45°，CD交AB于E，（1）求证：AD=CD；
（2）求AE的长．
如图，已知等腰Rt△ABC和等腰Rt△CDE，AC=BC，CD=CE，M、N分别为AE、BD的中点．
（1）判断CM与CN的位置关系和数量关系：
（2）若△CDE绕C旋转任意角度，其它条件不变，则（1）的结论是否仍成立？试证明．
查看习题详情和答案>>
（1）判断CM与CN的位置关系和数量关系：
（2）若△CDE绕C旋转任意角度，其它条件不变，则（1）的结论是否仍成立？试证明．
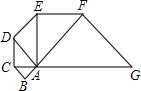如图，已知等腰Rt△ABC的直角边长为l，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推到第五个等腰Rt△AFG，则由这五个等腰直角三角形所构成的图形的面积为
如图，已知等腰Rt△ABC，∠ACB=90°，AC=BC，D为BC边上一动点，BC=nDC，AD⊥EC于点E，延长BE交AC与点F．