题目内容
如图,已知等腰Rt△ABC和等腰Rt△CDE,AC=BC,CD=CE,M、N分别为AE、BD的中点.
(1)判断CM与CN的位置关系和数量关系:
(2)若△CDE绕C旋转任意角度,其它条件不变,则(1)的结论是否仍成立?试证明.

(1)判断CM与CN的位置关系和数量关系:
(2)若△CDE绕C旋转任意角度,其它条件不变,则(1)的结论是否仍成立?试证明.

分析:(1)证△ACE≌△BCD,推出AE=BD,根据直角三角形斜边上中线得出CM=CN,推出∠MAC=∠MCA,∠NDC=∠NCD,即可得出答案;
(2)证△ACE≌△BCD,推出AE=BD,证△ECM≌△NDC,即可得出答案.
(2)证△ACE≌△BCD,推出AE=BD,证△ECM≌△NDC,即可得出答案.
解答:解:(1)CM=CN,MC⊥CN,
理由是:∵∠ACE=∠BCD=90°,
∴在△ACE和△BCD中
∴△ACE≌△BCD,
∴AE=BD,∠AEC=∠BDC,∠EAC=∠DBC,
∵∠ACE=∠BCD=90°,M为AE中点,N为BD中点,
∴CM=AM=ME=
AE,CN=DN=BN=
BD,
∴CM=CN,∠MAC=∠MCA,∠NDC=∠NCD,
∵∠AEC=∠BDC,∠EAC=∠DBC,
∴∠MCA+∠NCD=90°,
∴∠MCN=180°-90°=90°,
即MC⊥CN.
(2)成立,
证明:∵∠ACE=∠BCD=90°,∠ECB=∠ECB,
∴∠ECA=∠DCB,
∴在△ACE和△BCD中
∴△ACE≌△BCD,
∴AE=BD,∠AEC=∠BDC,
∵M、N分别为AE、BD中点,
∴EM=DN,
在△MEC和△NDC中
∴△MEC≌△NDC,
∴CM=CN,∠ECM=∠NCD,
∴∠MCN=∠ECM+∠ECN=∠NCD+∠ECN=∠ECD=90°,
∴CM⊥CN.
理由是:∵∠ACE=∠BCD=90°,
∴在△ACE和△BCD中
|
∴△ACE≌△BCD,
∴AE=BD,∠AEC=∠BDC,∠EAC=∠DBC,
∵∠ACE=∠BCD=90°,M为AE中点,N为BD中点,
∴CM=AM=ME=
| 1 |
| 2 |
| 1 |
| 2 |
∴CM=CN,∠MAC=∠MCA,∠NDC=∠NCD,
∵∠AEC=∠BDC,∠EAC=∠DBC,
∴∠MCA+∠NCD=90°,
∴∠MCN=180°-90°=90°,
即MC⊥CN.
(2)成立,
证明:∵∠ACE=∠BCD=90°,∠ECB=∠ECB,
∴∠ECA=∠DCB,
∴在△ACE和△BCD中
|
∴△ACE≌△BCD,
∴AE=BD,∠AEC=∠BDC,
∵M、N分别为AE、BD中点,
∴EM=DN,
在△MEC和△NDC中
|
∴△MEC≌△NDC,
∴CM=CN,∠ECM=∠NCD,
∴∠MCN=∠ECM+∠ECN=∠NCD+∠ECN=∠ECD=90°,
∴CM⊥CN.
点评:本题考查了全等三角形的性质和判定,直角三角形斜边上中线性质的应用,主要考查学生的推理能力.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 如图,已知等腰Rt△ABC,∠ACB=90°,AC=BC,D为BC边上一动点,BC=nDC,AD⊥EC于点E,延长BE交AC与点F.
如图,已知等腰Rt△ABC,∠ACB=90°,AC=BC,D为BC边上一动点,BC=nDC,AD⊥EC于点E,延长BE交AC与点F.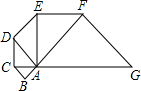 如图,已知等腰Rt△ABC的直角边长为l,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推到第五个等腰Rt△AFG,则由这五个等腰直角三角形所构成的图形的面积为
如图,已知等腰Rt△ABC的直角边长为l,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推到第五个等腰Rt△AFG,则由这五个等腰直角三角形所构成的图形的面积为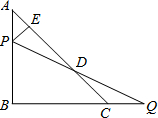 (2012•深圳二模)如图,已知等腰Rt△ABC中,∠B=90°,AB=BC=8cm,点P是线段AB上的点,点Q是线段BC延长线上的点,且AP=CQ,PQ与直线AC相交于点D.作PE⊥AC于点E,则线段DE的长度( )
(2012•深圳二模)如图,已知等腰Rt△ABC中,∠B=90°,AB=BC=8cm,点P是线段AB上的点,点Q是线段BC延长线上的点,且AP=CQ,PQ与直线AC相交于点D.作PE⊥AC于点E,则线段DE的长度( )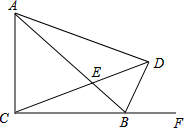 如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E,
如图,已知等腰Rt△ABC中,∠ACB=90°,AC=BC=4,D为△ABC的一个外角∠ABF的平分线上一点,且∠ADC=45°,CD交AB于E,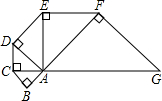 如图,已知等腰Rt△ABC直角边长为1,以它的斜边AC为直角边画第二个等腰Rt△ACD,再以斜边AD为直角边画第三个Rt△ADE…,依此类推,AC长为
如图,已知等腰Rt△ABC直角边长为1,以它的斜边AC为直角边画第二个等腰Rt△ACD,再以斜边AD为直角边画第三个Rt△ADE…,依此类推,AC长为