摘要: 已知:如图1.O为正方形ABCD的中心.分别延长OA到点F.OD到点E.使OF=2OA.OE=2OD.连结EF.将△FOE绕点O逆时针旋转α角得到△. (1) 探究AE′与BF'的数量关系.并给予证明, (2) 当α=30°时.求证:△AOE′为直角三角形. [答案](1)AE′=BF 证明:如图2. ∵在正方形ABCD中. AC⊥BD ∴∠=∠AOD=∠AOB=90° 即∠AOE′+∠AOF′=∠BOF′+∠AOF′ ∴∠AOE′=∠BOF′ 又∵OA=OB=OD.OE′=2OD.OF′=2OA ∴OE′=OF′ ∴△OAE′≌△OBF′ ∴AE′=BF (2)作△AOE′的中线AM.如图3. 则OE′=2OM=2OD=2OA ∴OA=OM ∵α=30° ∴∠AOM=60° ∴△AOM为等边三角形 ∴ MA=MO=ME′.∠=∠ 又∵∠+∠=∠AMO 即2∠=60° ∴∠=30° ∴∠+∠AOE′=30°+60°=90° ∴△AOE′为直角三角形.
网址:http://m.1010jiajiao.com/timu3_id_496558[举报]
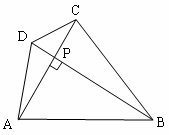
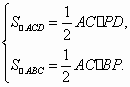

 已知:如图,PA,PB分别与⊙O相切于A,B点,C为⊙O上一点,∠ACB=65°,则∠APB等于( )
已知:如图,PA,PB分别与⊙O相切于A,B点,C为⊙O上一点,∠ACB=65°,则∠APB等于( )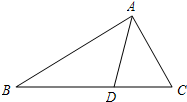 已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )
已知:如图,AD是△ABC的角平分线,且AB:AC=3:2,则△ABD与△ACD的面积之比为( )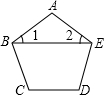 已知:如图,五边形的每一个内角都相等,连接对角线BE,且∠1=∠2,则∠1的度数是( )
已知:如图,五边形的每一个内角都相等,连接对角线BE,且∠1=∠2,则∠1的度数是( ) (1998•河北)已知:如图弦AB经过⊙O的半径OC的中点P,且AP=2,PB=3,则是⊙O的半径等于( )
(1998•河北)已知:如图弦AB经过⊙O的半径OC的中点P,且AP=2,PB=3,则是⊙O的半径等于( )