题目内容
已知抛物线的顶点是C(0,a)(a>0,a为常数),并经过点(2a,2a),点D(0,2a)为一定点.(1)求含有常数a的抛物线的解析式;
(2)设点P是抛物线上任意一点,过P作PH丄x轴.垂足是H,求证:PD=PH;
(3)设过原点O的直线l与抛物线在笫一象限相交于A、B两点,若DA=2DB.且S△ABD=4
| 2 |
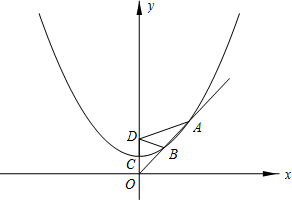
分析:(1)根据抛物线的图象假设出解析式为y=kx2+a,将经过点(2a,2a),代入求出即可;
(2)根据勾股定理得出PD2=DG2+PG2,进而求出PD=PH;
(3)利用(2)中结论得出BE=DB,AF=DA,即可得出B是OA的中点,进而得出S△OBD=S△ABD=4
,即可得出a的值.
(2)根据勾股定理得出PD2=DG2+PG2,进而求出PD=PH;
(3)利用(2)中结论得出BE=DB,AF=DA,即可得出B是OA的中点,进而得出S△OBD=S△ABD=4
| 2 |
解答:解:(1)设抛物线的解析式为y=kx2+a,
∵经过点(2a,2a),
4a2k+a=2a,
∴k=
,
则抛物线的解析式为:y=
x2+a;
(2)连接PD,设抛物线上一点P(x,y),过P作PH⊥x轴,PG⊥y轴,
在Rt△GDP中,由勾股定理得:PD2=DG2+PG2=(y-2a)2+x2=y2-4ay+4a2+x2,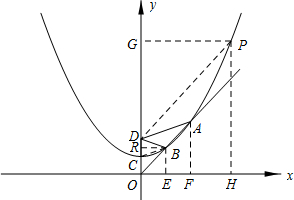
∵y=
x2+a,
∴x2=4a×(y-a)=4ay-4a2,
∴PD2=y2-4ay+4a2+4ay-4a2=y2=PH2,
∴PD=PH,
(3)过B作BE⊥x,AF⊥x,
由(2)的结论:BE=DB,AF=DA,
∵DA=2DB,
∴AF=2BE,
∴AO=2OB,
∴B是OA的中点,
∵C是OD的中点,
连接BC,∴BC=
=
=BE=DB,
过B作BR⊥y,
∵BR⊥CD,
∴CR=DR,OR=a+
=
,
∴
=
x2+a,
∴x2=2a2,
∵x>0,
∴x=
a,
∴B(
a,
),AO=2OB,
∴S△OBD=S△ABD=4
,
∴
×2a×
a=4
,
∴a2=4,
∵a>0,
∴a=2,
∵经过点(2a,2a),
4a2k+a=2a,
∴k=
| 1 |
| 4a |
则抛物线的解析式为:y=
| 1 |
| 4a |
(2)连接PD,设抛物线上一点P(x,y),过P作PH⊥x轴,PG⊥y轴,
在Rt△GDP中,由勾股定理得:PD2=DG2+PG2=(y-2a)2+x2=y2-4ay+4a2+x2,

∵y=
| 1 |
| 4a |
∴x2=4a×(y-a)=4ay-4a2,
∴PD2=y2-4ay+4a2+4ay-4a2=y2=PH2,
∴PD=PH,
(3)过B作BE⊥x,AF⊥x,
由(2)的结论:BE=DB,AF=DA,
∵DA=2DB,
∴AF=2BE,
∴AO=2OB,
∴B是OA的中点,
∵C是OD的中点,
连接BC,∴BC=
| AD |
| 2 |
| AF |
| 2 |
过B作BR⊥y,
∵BR⊥CD,
∴CR=DR,OR=a+
| a |
| 2 |
| 3a |
| 2 |
∴
| 3a |
| 2 |
| 1 |
| 4a |
∴x2=2a2,
∵x>0,
∴x=
| 2 |
∴B(
| 2 |
| 3a |
| 2 |
∴S△OBD=S△ABD=4
| 2 |
∴
| 1 |
| 2 |
| 2 |
| 2 |
∴a2=4,
∵a>0,
∴a=2,
点评:此题主要考查了二次函数的综合应用以及勾股定理的应用,二次函数的综合应用是初中阶段的重点题型,特别注意利用数形结合是这部分考查的重点,也是难点,同学们应重点掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目