摘要: 如图.在Rt△ABC中.∠ACB=90°.AC=6㎝.BC=8㎝.P为BC的中点.动点Q从点P出发.沿射线PC方向以2㎝/s的速度运动.以P为圆心.PQ长为半径作圆.设点Q运动的时间为t s. ⑴当t=1.2时.判断直线AB与⊙P的位置关系.并说明理由, ⑵已知⊙O为△ABC的外接圆.若⊙P与⊙O相切.求t的值. [答案]解:⑴直线与⊙P相切. 如图.过点P作PD⊥AB, 垂足为D. 在Rt△ABC中.∠ACB=90°.∵AC=6cm.BC=8cm. ∴.∵P为BC的中点.∴PB=4cm. ∵∠PDB=∠ACB=90°.∠PBD=∠ABC.∴△PBD∽△ABC. ∴,即.∴PD =2.4(cm) . 当时.(cm) ∴.即圆心到直线的距离等于⊙P的半径. ∴直线与⊙P相切. ⑵ ∠ACB=90°.∴AB为△ABC的外切圆的直径.∴. 连接OP.∵P为BC的中点.∴. ∵点P在⊙O内部.∴⊙P与⊙O只能内切. ∴或.∴=1或4. ∴⊙P与⊙O相切时.t的值为1或4.
网址:http://m.1010jiajiao.com/timu3_id_496019[举报]
 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E,AE=2cm,则BC=
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E,AE=2cm,则BC= 如图,在Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC,过点D作AB的垂线交AC于点E,CD交BE于点F.
如图,在Rt△ABC中,∠ACB=90°,D是AB上的一点,BD=BC,过点D作AB的垂线交AC于点E,CD交BE于点F.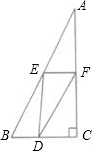 如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4,E是AB边的中点,F是AC边的中点,则(1)EF=
如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4,E是AB边的中点,F是AC边的中点,则(1)EF=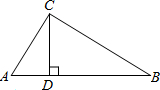 (2012•乐山模拟)如图,在Rt△ABC中,∠C=90°,两直角边AC、BC的长恰是方程x2-4x+2=0的两个不同的根,则Rt△ABC的斜边上的高线CD的长为( )
(2012•乐山模拟)如图,在Rt△ABC中,∠C=90°,两直角边AC、BC的长恰是方程x2-4x+2=0的两个不同的根,则Rt△ABC的斜边上的高线CD的长为( ) 如图,在Rt△ABC中,∠ACB=90°,AB=12,CD是AB边上的中线,则CD的长为( )
如图,在Rt△ABC中,∠ACB=90°,AB=12,CD是AB边上的中线,则CD的长为( )