摘要: 已知二次函数,当自变量x取m时,对应的函数值大于0,当自变量x分别取m-1,m+1时对应的函数值.,则必值,满足 ( ) A. >0,>0 B. <0,<0 C.<0,>0 D.>0,<0 答案[B ]
网址:http://m.1010jiajiao.com/timu3_id_495370[举报]
已知二次函数![]() ,当自变量x取m时,对应的函数值大于0,当自变量x分别取m-1,m+1时对应的函数值
,当自变量x取m时,对应的函数值大于0,当自变量x分别取m-1,m+1时对应的函数值![]() 、
、![]() ,则必值
,则必值![]() ,
,![]() 满足 ( )
满足 ( )
A. ![]() >0,
>0,![]() >0 B.
>0 B. ![]() <0,
<0,![]() <0 C.
<0 C.![]() <0,
<0,![]() >0 D.
>0 D.![]() >0,
>0,![]() <0
<0
请阅读下面材料:
若 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.
为此抛物线的对称轴.
有一种方法证明如下:
|
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点, ∴
(a ≠ 0)上不同的两点, ∴ 且
且  ≠
≠ .
. ①-②得
 .
.∴
 .
.∴
 .
.又∵ 抛物线
 (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为 ,
,∴ 直线
 为此抛物线的对称轴.
为此抛物线的对称轴.(1)反之,如果
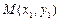 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,直线
(a ≠ 0)上不同的两点,直线 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取 ,
, 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;(2)利用以上结论解答下面问题:
已知二次函数
 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
查看习题详情和答案>>
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
查看习题详情和答案>>
请阅读下面材料:
若![]() ,
,![]() 是抛物线
是抛物线![]() (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线![]() 为此抛物线的对称轴.
为此抛物线的对称轴.
有一种方法证明如下:
|
∴  且
且 ![]() ≠
≠![]() .
.
①-②得 ![]() .
.
∴ ![]() .
.
∴ ![]() .
.
又∵ 抛物线![]() (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为![]() ,
,
∴ 直线![]() 为此抛物线的对称轴.
为此抛物线的对称轴.
(1)反之,如果![]() ,
,![]() 是抛物线
是抛物线![]() (a ≠ 0)上不同的
(a ≠ 0)上不同的
两点,直线![]() 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取![]() ,
,![]() 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
(2)利用以上结论解答下面问题:
已知二次函数![]() 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
请阅读下面材料:
若 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.
为此抛物线的对称轴.
有一种方法证明如下:
证明:∵ ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点, ∴
(a ≠ 0)上不同的两点, ∴ 且
且  ≠
≠ .
.
①-②得 .
.
∴ .
.
∴ .
.
又∵ 抛物线 (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为 ,
,
∴ 直线 为此抛物线的对称轴.
为此抛物线的对称轴.
(1)反之,如果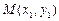 ,
,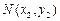 是抛物线
是抛物线 (a ≠ 0)上不同的两点,直线
(a ≠ 0)上不同的两点,直线 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取 ,
, 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
(2)利用以上结论解答下面问题:
已知二次函数 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
查看习题详情和答案>>
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
查看习题详情和答案>>
若
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点,证明直线
(a ≠ 0)上不同的两点,证明直线 为此抛物线的对称轴.
为此抛物线的对称轴.有一种方法证明如下:
|
 ,
, 是抛物线
是抛物线 (a ≠ 0)上不同的两点, ∴
(a ≠ 0)上不同的两点, ∴ 且
且  ≠
≠ .
. ①-②得
 .
.∴
 .
.∴
 .
.又∵ 抛物线
 (a ≠ 0)的对称轴为
(a ≠ 0)的对称轴为 ,
,∴ 直线
 为此抛物线的对称轴.
为此抛物线的对称轴.(1)反之,如果
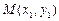 ,
,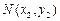 是抛物线
是抛物线 (a ≠ 0)上不同的两点,直线
(a ≠ 0)上不同的两点,直线 为该抛物线的对称轴,那么自变量取
为该抛物线的对称轴,那么自变量取 ,
, 时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;
时函数值相等吗?写出你的猜想,并参考上述方法写出证明过程;(2)利用以上结论解答下面问题:
已知二次函数
 当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
查看习题详情和答案>>
当x = 4 时的函数值与x = 2007 时的函数值相等,求x = 2012时的函数值.
查看习题详情和答案>>