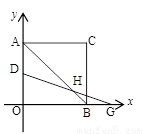
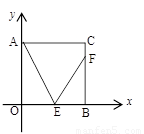
摘要: 如图所示.在平面直角坐标系xOy中.正方形OABC的边长为2cm.点A.C分别在y轴的负半轴和x轴的正半轴上.抛物线y=ax2+bx+c经过点A.B和D. (1)求抛物线的解析式. (2)如果点P由点A出发沿AB边以2cm/s的速度向点B运动.同 时点Q由点B出发沿BC边以1cm/s的速度向点C运动.当其中一点到达终点时.另一点也随之停止运动. 设S=PQ2(cm2) ①试求出S与运动时间t之间的函数关系式.并写出t的取值范围, ②当S取时.在抛物线上是否存在点R.使得以P.B.Q.R为顶点的四边形是平行四边形? 如果存在.求出R点的坐标,如果不存在.请说明理由. (3)在抛物线的对称轴上求点M.使得M到D.A的距离之差最大.求出点M的坐标. 二0一一年福州市初中毕业会考.高级中等学校招生考试
网址:http://m.1010jiajiao.com/timu3_id_494025[举报]
(本题满分为14分)平面直角坐标系中,正方形AOBC如图所示,点C的坐标为(a,a),其中a使得式子![]() 有意义,反比例函数
有意义,反比例函数![]() 的图象经过点C.
的图象经过点C.
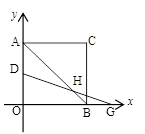
(1)求反比例函数解析式.
(2)若有一点D自A向O运动,且满足AD2=OD·AO,求此时D点坐标.
(3)若点D在AO上、G为OB的延长线上的点,AD=BG,连接AB交DG于点H,写出AB-2HB与AD之间的数量关系(直接写出不需证明).
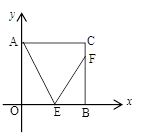
(4)如图,点E为正方形AOBC的OB边一点,点F为BC上一点且∠CAE=∠FEA=60°,求直线EF的解析式.
查看习题详情和答案>>
(本题满分为14分)平面直角坐标系中,正方形AOBC如图所示,点C的坐标为(a,a),其中a使得式子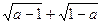 有意义,反比例函数
有意义,反比例函数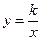 的图象经过点C.
的图象经过点C.
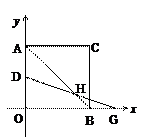
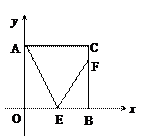
(1)求反比例函数解析式.
(2)若有一点D自A向O运动,且满足AD2=OD·AO,求此时D点坐标.
(3)若点D在AO上、G为OB的延长线上的点,AD=BG,连接AB交DG于点H,写出AB-2HB与AD之间的数量关系(直接写出不需证明).
(4)如图,点E为正方形AOBC的OB边一点,点F为BC上一点且∠CAE=∠FEA=60°,求直线EF的解析式. 查看习题详情和答案>>
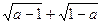 有意义,反比例函数
有意义,反比例函数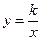 的图象经过点C.
的图象经过点C.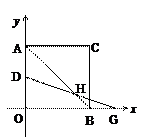
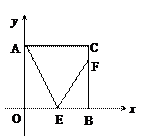
(1)求反比例函数解析式.
(2)若有一点D自A向O运动,且满足AD2=OD·AO,求此时D点坐标.
(3)若点D在AO上、G为OB的延长线上的点,AD=BG,连接AB交DG于点H,写出AB-2HB与AD之间的数量关系(直接写出不需证明).
(4)如图,点E为正方形AOBC的OB边一点,点F为BC上一点且∠CAE=∠FEA=60°,求直线EF的解析式. 查看习题详情和答案>>
 有意义,反比例函数
有意义,反比例函数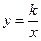 的图象经过点C.
的图象经过点C.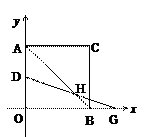

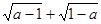 有意义,反比例函数
有意义,反比例函数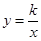 的图象经过点C.
的图象经过点C.