题目内容
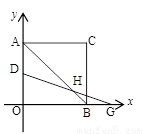
(本题满分为14分)平面直角坐标系中,正方形AOBC如图所示,点C的坐标为(a,a),其中a使得式子![]() 有意义,反比例函数
有意义,反比例函数![]() 的图象经过点C.
的图象经过点C.
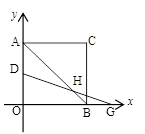
(1)求反比例函数解析式.
(2)若有一点D自A向O运动,且满足AD2=OD·AO,求此时D点坐标.
(3)若点D在AO上、G为OB的延长线上的点,AD=BG,连接AB交DG于点H,写出AB-2HB与AD之间的数量关系(直接写出不需证明).
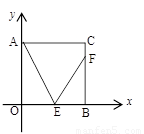
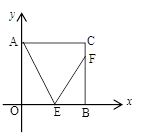
(4)如图,点E为正方形AOBC的OB边一点,点F为BC上一点且∠CAE=∠FEA=60°,求直线EF的解析式.
(1)![]()
把C(1,1)代入![]() ∴
∴![]() (3分)
(3分)
(2)OA=1,OD=1-AD AD2=OD·AO=1·(1-AD)
AD2+AD-1=0 AD=![]() ∵AD>0 ∴AD=
∵AD>0 ∴AD=![]()
OD=![]() 故D(0,
故D(0,![]() )(7分)
)(7分)
(3)AB-2HB=![]() AD(10分)
AD(10分)
(4)∵∠CAE=∠FEA=60° ∴∠OAE=30° OA=1,设OE=x,则AE=2x
![]() 解得
解得![]() ,OE=
,OE=![]()
∠BEF=180°-∠OEA-∠AEF=60° BE=1-OE=1![]() FE=2
FE=2![]()
BF=![]() ∴E(
∴E(![]() ) F(1,
) F(1,![]() )
)
设解析式为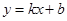
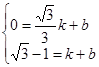 解得
解得![]()
∴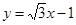
解析:略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
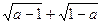 有意义,反比例函数
有意义,反比例函数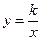 的图象经过点C.
的图象经过点C.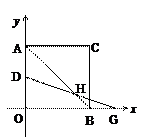
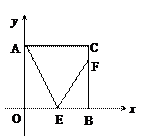
 有意义,反比例函数
有意义,反比例函数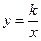 的图象经过点C.
的图象经过点C.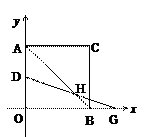

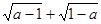 有意义,反比例函数
有意义,反比例函数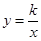 的图象经过点C.
的图象经过点C.