摘要: 如图1.在直角坐标系xoy中.O是坐标原点.点A在x正半轴上.OA=12cm.点B在y轴的正半轴上.OB=12cm.动点P从点O开始沿OA以2cm/s的速度向点A移动.动点Q从点A开始沿AB以4cm/s的速度向点B移动.动点R从点B开始沿BO以2cm/s的速度向点O移动.如果P.Q.R分别从O.A.B同时移动.移动时间为ts. (1)求∠OAB的度数. (2)以OB为直径的⊙O′与AB交于点M.当t为何值时.PM与⊙O′相切? (3)是否存在△RPQ为等腰三角形?若存在.请直接写出t值,若不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_492703[举报]
(本题满分10分)如图,在平面直角坐标系 中,把抛物线
中,把抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
(1)写出![]() 的值;
的值;
(2)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ∽
∽![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.

查看习题详情和答案>>
(本题满分10分)如图,在平面直角坐标系 中,把抛物线
中,把抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于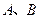 两点(点
两点(点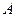 在点
在点 的左边),与
的左边),与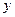 轴交于点
轴交于点 ,顶点为
,顶点为 .
.
(1)写出 的值;
的值;
(2)判断 的形状,并说明理由;
的形状,并说明理由;
(3)在线段 上是否存在点
上是否存在点 ,使
,使 ∽
∽ ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由. 查看习题详情和答案>>
查看习题详情和答案>>
 中,把抛物线
中,把抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于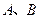 两点(点
两点(点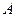 在点
在点 的左边),与
的左边),与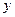 轴交于点
轴交于点 ,顶点为
,顶点为 .
.(1)写出
 的值;
的值;(2)判断
 的形状,并说明理由;
的形状,并说明理由;(3)在线段
 上是否存在点
上是否存在点 ,使
,使 ∽
∽ ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由. 查看习题详情和答案>>
查看习题详情和答案>>
(本题满分10分)如图,在平面直角坐标系 中,把抛物线
中,把抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于 两点(点
两点(点 在点
在点 的左边),与
的左边),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
.
(1)写出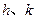 的值;
的值;
(2)判断 的形状,并说明理由;
的形状,并说明理由;
(3)在线段 上是否存在点
上是否存在点 ,使
,使
 ∽
∽ ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
 中,把抛物线
中,把抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于 两点(点
两点(点 在点
在点 的左边),与
的左边),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
. 的值;
的值; 的形状,并说明理由;
的形状,并说明理由; 上是否存在点
上是否存在点 ,使
,使 ∽
∽ ?若存在,求出点
?若存在,求出点